1．知识技能

①对数函数的概念，熟悉对数函数的图象与性质规律.

②掌握对数函数的性质，能初步运用性质解决问题.

2、思考：(1)证明和应用对数运算性质时，应注意哪些问题？

　　　　 (2)

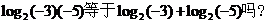
4、作业

(1)书面作业：P₈₆　习题2.2　第3、4题　　 P₈₇第11、12题

3、归纳小结

(1)学习归纳本节

(2)你认为学习对数有什么意义？大家议论.

2．讲授新课

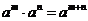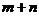探究：在上课中，我们知道，对数式可看作指数运算的逆运算，你能从指数与对数的关系以及指数运算性质，得出相应的对数运算性质吗？如我们知道，那如何表示，能用对数式运算吗？

如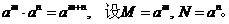：于是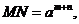 由对数的定义得到

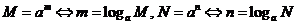
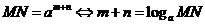
即：同底对数相加，底数不变，真数相乘

提问：你能根据指数的性质按照以上的方法推出对数的其它性质吗？

(让学生探究，讨论)

如果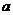＞0且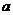≠1，M＞0，N＞0，那么：

(1)

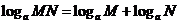
(2)

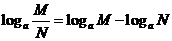
(3)

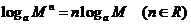
证明：

(1)令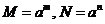

　　 则：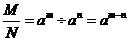　

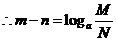
又由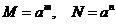

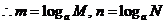
即：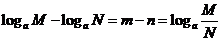

(3)

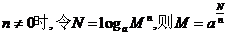
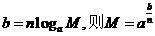
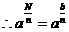
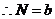
即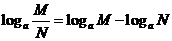

当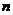=0时，显然成立.

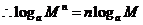
提问：1. 在上面的式子中，为什么要规定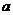＞0，且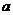≠1，M＞0，N＞0？

1．设置情境

复习：对数的定义及对数恒等式

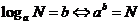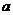　 (＞0，且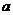≠1，N＞0)，

指数的运算性质.

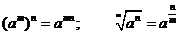
学法：学生自主推理、讨论和概括，从而更好地完成本节课的教学目标.

教学用具：投影仪

重点：对数运算的性质与对数知识的应用

难点：正确使用对数的运算性质

3. 情感、态度、和价值观

让学生感觉对数运算性质的重要性，增加学生的成功感，增强学习的积极性.