
3.情感、态度、价值观
(1)提高学生的认知水平,为学生塑造良好的数学认识结构.
(2)培养学生数形结合的思想观念及抽象思维能力.
2.过程与方法
通过提问,分析点评,让学生更能熟悉指数函数,对数函数的性质.
1.知识与技能
(1)理解指数与对数,指数函数与对数函数的联系.
(2)能更加熟练地解决与指数函数,对数函数有关的问题.
6.归纳小结:提问方式
(1)我们今天学习了哪一类基本函数,它们定义是怎样描述的?
(2)你能根据函数图象说出有关幂函数的性质吗?
作业:P92 习题 2.3 第2、3 题
5.课堂练习
画出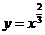 的大致图象,并求出其定义域、奇偶性,并判断和证明其单调性.
的大致图象,并求出其定义域、奇偶性,并判断和证明其单调性.
2.利用函数的性质 ,判断下列两个值的大小
(1)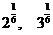 (2)
(2)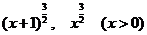 (3)
(3)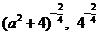
分析:利用幂函数的单调性来比较大小.
1.证明幂函数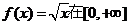 上是增函数
上是增函数
证:任取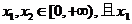 <
< 则
则
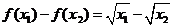
=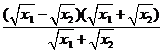
=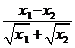
因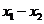 <0,
<0,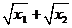 >0
>0
所以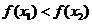 ,即
,即 上是增函数.
上是增函数.
思考:
我们知道,若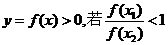 得
得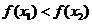 ,你能否用这种作比的方法来证明
,你能否用这种作比的方法来证明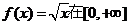 上是增函数,利用这种方法需要注意些什么?
上是增函数,利用这种方法需要注意些什么?
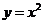 引导学生用列表描点法,应用函数的性质,如奇偶性,定义域等,画出函数图像,最后,教师利用电脑软件画出以上五个数数的图像.
引导学生用列表描点法,应用函数的性质,如奇偶性,定义域等,画出函数图像,最后,教师利用电脑软件画出以上五个数数的图像.
|
|
|
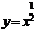
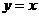
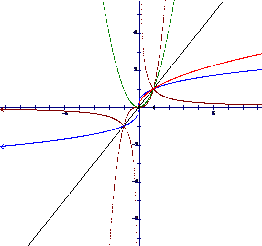
让学生通过观察图像,分组讨论,探究幂函数的性质和图像的变化规律,教师注意引导学生用类比研究指数函数,对函数的方法研究幂函数的性质.
通过观察图像,填P91探究中的表格
|
|
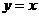 |
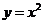 |
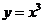 |
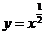 |
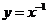 |
|
定义域 |
R |
R |
R |
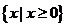 |
 |
|
奇偶性 |
奇 |
奇 |
奇 |
非奇非偶 |
奇 |
|
在第Ⅰ象限单调增减性 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递增 |
在第Ⅰ象限单调递减 |
|
定点 |
(1,1) |
(1,1) |
(1,1) |
(1,1) |
(1,1) |
3.幂函数性质
(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1)(原因: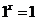 );
);
(2)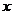 >0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(从左往右看,函数图象逐渐上升).
>0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(从左往右看,函数图象逐渐上升).
特别地,当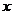 >1,
>1,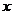 >1时,
>1时,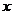 ∈(0,1),
∈(0,1),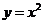 的图象都在
的图象都在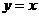 图象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)
图象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)
当∠α<1时,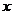 ∈(0,1),
∈(0,1),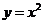 的图象都在
的图象都在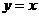 的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)
的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)
(3)α<0时,幂函数的图象在区间(0,+∞)上是减函数.
在第一家限内,当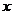 向原点靠近时,图象在
向原点靠近时,图象在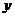 轴的右方无限逼近
轴的右方无限逼近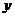 轴正半轴,当
轴正半轴,当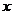 慢慢地变大时,图象在
慢慢地变大时,图象在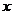 轴上方并无限逼近
轴上方并无限逼近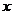 轴的正半轴.
轴的正半轴.
例题:
2.研究函数的图像
(1)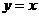 (2)
(2)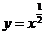 (3)
(3)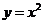
(4)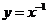 (5)
(5)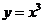
1.幂函数的定义
一般地,形如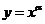 (
(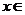 R)的函数称为幂孙函数,其中
R)的函数称为幂孙函数,其中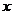 是自变量,
是自变量,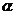 是常数.
是常数.
如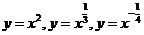 等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.
等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com