4. 教材对幂函数的内容做了削减，仅限于学习五种学生易于掌握的幂函数，并且安排的顺序向后调整，教学中应防止增加这部分内容，以免增加学生学习的负担.

3、教材对反函数的学习要求仅限于初步知道概念，目的在于强化指数函数与对数函数这两种函数模型的学习，教学中不宜对其定义做更多的拓展 .

2. 在学习对数函数的图象和性质时，教材将它与指数函数的有关内容做了比较，让学生体会两种函数模型的增长区别与关联，渗透了类比思想. 建议教学中重视知识间的迁移与互逆作用.

1. 教材注重从现实生活的事例中引出指数函数概念，所举例子比较全面，有利于培养学生的思想素质和激发学生学习数学的兴趣和欲望. 教学中要充分发挥课本的这些材料的作用，并尽可能联系一些熟悉的事例，以丰富教学的情景创设.

8. 通过实例，了解幂函数的概念，结合五种具体函数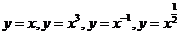的图象，了解它们的变化情况 .

7. 知道指数函数y=a^x与对数函数y=log_ax互为反函数(a＞0, a≠1)，初步了解反函数的概念和f^{- -1}(x)的意义.

6. 通过具体函数，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，掌握f(x)=log_ax符号及意义，体会对数函数是一类重要的函数模型，能借助计算器或计算机画出具体对数函数的图象，探索并了解对数函数的有关性质(单调性、值域、特殊点).

4. 通过应用实例的教学，体会指数函数是一种重要的函数模型.

3. 理解指数函数的概念和意义，掌握f(x)=a^x的符号、意义，能借助计算器或计算机画出具体指数函数的图象，探索并理解指数函数的有关性质(单调性、值域、特别点).