6．(2009·巢湖期末)给出下列命题：

①函数y＝cos是奇函数；

②存在实数α，使得sin α+cos α＝；

③若α、β是第一象限角且α<β，则tan α<tan β；

④x＝是函数y＝sin的一条对称轴方程；

⑤函数y＝sin的图象关于点成中心对称图形．

其中正确的序号为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．①③　 　　　　　　　 B．②④　 　　　　　　　　　 C．①④ 　　　　　　　　　　 　D．④⑤

解析　①y＝cos⇒y＝－sinx是奇函数；

②由sin α+cos α＝sin的最大值为，

因为<，所以不存在实数α，使得sin α+cos α＝；

③α，β是第一象限角且α<β.例如：45°<30°+360°，

但tan 45°>tan(30°+360°)，即tan α<tan β不成立；

④把x＝代入y＝sin＝sin＝－1，所以x＝是函数y＝sin的一条对称轴；

⑤把x＝代入y＝sin＝sin＝1，

所以点不是函数y＝sin的对称中心．

综上所述，只有①④正确．

答案　C

5．(2009·浙江理，8)已知a是实数，则函数f(x)＝1+asin ax的图象不可能是　　　　　 `(　)

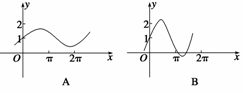
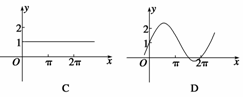
解析　图A中函数的最大值小于2，故0<a<1，而其周期大于2π.故A中图象可以是函数f(x)的图象．图B中，函数的最大值大于2，故a应大于1，其周期小于2π，故B中图象可以是函数f(x)的图象．当a=0时，f(x)=1，此时对应C中图象，对于D可以看出其最大值大于2，其周期应小于2π，而图象中的周期大于2π，故D中图象不可能为函数f(x)的图象．

答案　D

4．(2010·嘉兴模拟)已知在函数f(x)＝sin 图象上，相邻的一个最大值点与一个最小值点

恰好在x²+y²＝R²上，则f(x)的最小正周期为　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1　 　　　　　　　　　　　　　 B．2 　　　　　　　　　　　　 C．3　 　　　　　　　　 D．4

解析　∵x²+y²＝R²，∴x∈[－R，R]．

∵函数f(x)的最小正周期为2R，

∴最大值点为，

相邻的最小值点为，

代入圆方程，得R＝2，∴T＝4.

答案　D

3．(2010·枣庄调研)已知函数y＝sin 在区间[0，t]上至少取得2次最大值，则正整数t的最

小值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．6　 　　　　　　　　　　　　　 B．7 　　　　　　　　　　　　 C．8　 　　　　　　　　 D．9

解析　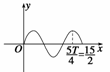T=6，则≤t，

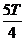∴t≥，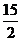

∴tmin=8.

答案　C

0.∴+φ＝kπ+(k∈Z)．∴φ＝kπ+－(k∈Z)．

|φ|的最小值为＝.

答案　A

2．(2009·全国Ⅰ理，8)如果函数y＝3cos(2x+φ)的图象关于点中心对称，那么|φ|的最

小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　 B.　 　　　　　　　　　　　　　 C.　 　　　　　　　　　　 D.

解析　由y＝3cos(2x+φ)的图象关于点中心对称知，f＝0，即3cos＝

1．(2009·福建理，1)函数f(x)＝sin xcos x的最小值是　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－1　 　　　　　　　　　　　　 B．－ 　　　　　　　 　　　 C.　 　　　　　　　　　　 D．1

解析　∵f(x)＝sin xcos x＝sin 2x.

∴当x＝kπ－，k∈Z时，f(x)_min＝－.

答案　B

12．(14分)(2009·丽水联考)是否存在角α，β，其中α∈(－，)，β∈(0，π)，使得等式sin(3π

－α)＝cos(－β)，cos(－α)＝－cos(π+β)同时成立．若存在，求出α，β的值；若不存在，请说明理由．

解　假设满足题设要求的α，β存在，则α，β满足

①²+②²，得sin²α+3(1－sin²α)＝2，

即sin²α＝，sin α＝±.

∵－<α<，∴α＝或α＝－.

(1)当α＝时，由②得cos β＝，

∵0<β<π，∴β＝.

(2)当α＝－时，由②得cos β＝，β＝，但不适合①式，故舍去．

综上可知，存在α＝，β＝使两个等式同时成立．

§4.3　三角函数的图象与性质

11．(13分)(2010·菏泽模拟)已知sin(π－α)－cos(π+α)＝.求下列各式的值：

(1)sin α－cos α；

(2)sin³+cos³.

解　由sin(π－α)－cos(π+α)＝，

得sin α+cos α＝.①

将①式两边平方，得1+2sin α·cos α＝，

故2sin α·cos α＝－，

又<α<π，∴sin α>0，cos α<0.

∴sin α－cos α>0.

(1)(sin α－cos α)²＝1－2sin α·cos α＝1－＝，

∴sin α－cos α＝.

(2)sin³+cos³＝cos³α－sin³α

＝(cos α－sin α)(cos²α+cos α·sin α+sin²α)

＝×＝－.

10．(13分)(2010·揭阳联考)已知sin(3π+θ)＝，求+

的值．

解　∵sin(3π+θ)＝－sin θ＝，∴sin θ＝－，

∴原式＝+

＝+

＝+＝

＝＝＝18.