12．(2008·江苏)某地有三家工厂，分别位于矩形ABCD的顶点A，B及CD的中点P处，已知AB＝20 km，CB＝10 km，为了处理三家工厂的污水，现要在矩形ABCD的区域上(含边界)，且A，B与等距离的一点O处建造一个污水处理厂，并铺设排污管道AO，BO，OP，设排污管道的总长为y km.

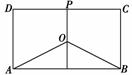
(1)按下列要求写出函数关系式：

①设∠BAO＝θ(rad)，将y表示成θ的函数关系式；

②设OP＝x(km)，将y表示成x的函数关系式．

(2)请你选用(1)中的一个函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短．

[解]　本小题主要考查函数最值的应用．

(1)①由条件知PQ垂直平分AB，若∠BAO＝θ(rad)，则OA＝＝，故OB＝，又OP＝10－10 tanθ，

所以y＝OA+OB+OP＝++10－10tanθ，

所求函数关系式为y＝+10(0＜θ＜)

②若OP＝x(km)，则OQ＝10－x，所以OA＝OB＝＝

所求函数关系式为y＝x+2(0＜x＜10)

(2)选择函数模型①，

y′＝

＝

令y′＝0得sinθ＝，因为0＜θ＜，所以θ＝，

当θ∈(0，)时，y′＜0，y是θ的减函数；当θ∈(，)时，y′＞0，y是θ的增函数，所以当θ＝时，y_min＝10+10.这时点P位于线段AB的中垂线上，且距离AB边km处．

亲爱的同学请写上你的学习心得

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

11．某造船公司年造船量是20艘，已知造船x艘的产值函数为R(x)＝3700x+45x²－10x³(单位：万元)，成本函数为C(x)＝460x+5000(单位：万元)，又在经济学中，函数f(x)的边际函数Mf(x)定义为Mf(x)＝f(x+1)－f(x)．

(1)求利润函数P(x)及边际利润函数MP(x)；(提示：利润＝产值－成本)

(2)问年造船量安排多少艘时，可使公司造船的年利润最大？

(3)求边际利润函数MP(x)的单调递减区间，并说明单调递减在本题中的实际意义是什么？

[解]　(1)P(x)＝R(x)－C(x)

＝－10x³+45x²+3240x－5000(x∈N^*，且1≤x≤20)；

MP(x)＝P(x+1)－P(x)

＝－30x²+60x+3275(x∈N^*，且1≤x≤19)．

(2)P′(x)＝－30x²+90x+3240

＝－30(x－12)(x+9)，

∵x＞0，∴P′(x)＝0时，x＝12，

∴当0＜x＜12时，P′(x)＞0，

当x＞12时，P′(x)＜0，

∴x＝12时，P(x)有最大值．

即年造船量安排12艘时，可使公司造船的年利润最大．

(3)MP(x)＝－30x²+60x+3275＝－30(x－1)²+3305.

所以，当x≥1时，MP(x)单调递减，

所以单调减区间为[1,19]，且x∈N^*.

MP(x)是减函数的实际意义是：随着产量的增加，每艘利润与前一艘比较，利润在减少．

10．某厂生产某种产品x件的总成本c(x)＝1200+x²(万元)，已知产品单价的平方与产品件数x成反比，生产100件这样的产品单价为50万元，则产量定为________件时总利润最大．

[答案]　25

9．如右图所示，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正六棱柱容器．当这个正六棱柱容器的底面边长为________时，其容积最大．

[分析]　本小题主要考查正六棱柱的概念与性质，以及函数的相关知识，考查学生运用导数知识解决实际问题的能力．

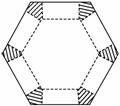
[解析]　设被切去的全等四边形的一边长为x(如图所示)则正六棱柱的底面边长为1－2x，高为x，所以正六棱柱的体积V＝6×(1－2x)²×x(0＜x＜)，化简得V＝(4x³－4x²+x)．

又V′＝(12x²－8x+1)，

由V′＝0，得x＝或x＝.

∵当x∈(0，)时，V′＞0，V是增函数；

当x∈(，)时，V′＜0，V是减函数．

∴当x＝时，V有最大值，正六棱柱的底面边长为.

[答案]　

8．用总长为14.8 m的钢条制作一个长方体容器的框架，若所制作容器的底面的一边比高长0.5 m，则当高为________米时，容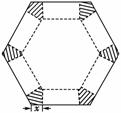器的面积最大．

[解析]　设容器的高为x米，则V＝x(x+0.5)(3.2－2x)，

V′＝－6x²+4.4x+1.6＝0，解15x²－11x－4＝0，x＝1(x＝－舍去)．

[答案]　1

7．某宾馆有50个房间供游客居住，当每个房间定价为每天180元时，房间会全部住满；房间单价每增加10元，就会有一个房间空闲．如果游客居住房间，宾馆每间每天需花费20元的各种维护费用，要使宾馆利润最大，房间应定价________元．

[解析]　设每个房间每天的定价为x元，那么宾馆利润

l(x)＝(50－)(x－20)＝－x²+70x+1360，令l′(x)＝－x+70＝0，解得x＝350.l(x)只有一个极值，且为极大值，所以x＝350为最大值点．

[答案]　350

6．某公司生产某种产品，固定成本为20000元，每生产一单位产品，成本增加100元，已知总收益R与年产量x的关系是R＝R(x)＝，则总利润最大时，每年生产的产品是

(　)

A．100　 　　　　　　　　　　　　　 B．150

C．200　 　　　　　　　　　　　　　　 D．300

[解析]　由题意得，总成本函数为

C＝C(x)＝20000+100x，所以总利润函数为

P＝P(x)＝R(x)－C(x)

＝

而P′(x)＝

令P′(x)＝0，得x＝300，易知x＝300时，P最大．

[答案]　D