2、在100mL 36.5%的浓盐酸(密度为1.18g/cm³)中加入多少mL 2mol/L的稀盐酸(密度为1.08g/cm³)，才能配成6mol/L的盐酸(密度为1.10g/cm³)。

　解析：任何溶液在稀释时，溶液和溶剂的量都要发生变化，但溶质的量不变，据此可以得到稀释下列各种浓度的溶液计算公式。

　 百分比浓度溶液的稀释公式：

　 浓溶液的质量×浓溶液的浓度 = 稀溶液的质量×稀溶液的浓度

　 mol尔浓度的溶液稀释公式：

　 浓溶液的浓度×浓溶液的体积(L) = 稀溶液的浓度×稀溶液的体积

　 同一溶质的两种不同浓度的溶液混合时，混合溶液的浓度介于溶液之间，混合液跟两原溶液中溶质、溶液量的基本关系是：

　 (1)混合液中所含溶质的总量等于两原溶液的溶质质量之和。

　 (2)混合溶液的质量等于两原溶液的质量之和，但体积不等于两原溶液的体积之和(当两原溶液很稀时，通常把混合液的体积近似地看做两原溶液的体积之和。)

　 在应用上述关系进行复杂的混合溶液计算时，可先算出混合溶液的总质量和溶质的总质量，然后再求出混合溶液的浓度。

　 设需加入VmL 2mol/L的盐酸

　 混合液中溶质的总物质的量

　 混合溶液的总体积：

　 混合液的物质的量浓度：

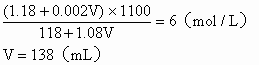
1、金属锡的纯度可以通过下述方法分析：将试样溶于盐酸，反应的化学方程式为：Sn+2HCl=SnCl₂+H₂再加入过量的FeCl溶液，发生如下反应：SnCl₂+2FeCl=SnCl₄+2FeCl₂最后用已知浓度的K₂Cr₂O₇溶液滴定生成Fe²⁺，反应的化学方程式为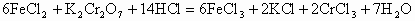：现有金属锡试样0.613g，经上述反应后，共用去0.100 mol/LK₂Cr₂O₇溶液16.0mL。求试样中锡的百分含量(假定杂质不参加反应)。

解析：该题是应用关系式法解多步反应的综合计算。根据题目所给出的三个化学反应，得出Sn与K₂Cr₂O₇的物质量的关系。

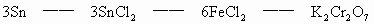
13.图示中滑块和小球的质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点O由一不可伸长的轻绳相连，轻绳长为l.开始时，轻绳处于水平拉直状态，小球和滑块均静止.现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有黏性物质的固定挡板粘住，在极短的时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向的夹角θ＝60° 时小球达到最高点.求：

(1)从滑块与挡板接触到速度刚好变为零的过程中，挡板阻力对滑块的冲量.

(2)小球从释放到第一次到达最低点的过程中，绳的拉力对小球做功的大小.[2008年高考·全国理综卷Ⅰ]

解析：(1)解法一　设小球摆至最低点时，滑块和小球的速度大小分别为v₁、v₂，对于滑块和小球组成的系统，由机械能守恒定律得：mv+mv＝mgl

同理，滑块被粘住后，对于小球向左摆动的过程，有：

mv＝mgl(1－cos 60°)

解得：v₁＝v₂＝

对于滑块与挡板接触的过程，由动量定理得：

I＝0－mv₁

挡板对滑块的冲量I＝－m，负号表示方向向左.

解法二　设小球摆至最低点时，滑块和小球的速度大小分别为v₁、v₂，由动量守恒定律得：

mv₁－mv₂＝0

对于小球向左摆动的过程，由机械能守恒定律得：

mv＝mgl(1－cos 60°)

解得：v₁＝v₂＝

对于滑块与挡板接触的过程，由动量定理有：

I＝0－mv₁

解得挡板对滑块的冲量为：

I＝－m，负号表示方向向左.

解法三　设小球摆至最低点时，滑块和小球的速度大小分别为v₁、v₂，由机械能守恒定律得：

mv+mv＝mgl

又由动量守恒定律得：

mv₁+m(－v₂)＝0

解得：v₁＝v₂＝

对于滑块与挡板接触的过程，由动量定理得：

I＝0－mv₁解得挡板对滑块的冲量为：

I＝－m，负号表示方向向左.

　解法四　由全过程的能量转换和守恒关系可得(滑块在碰撞时损失的能量等于系统机械能的减少量，等于滑块碰前的动能)：

ΔE＝mgl－mgl(1－cos 60°)＝mv²

解得滑块碰前的速度为：v＝

对于滑块与挡板接触的过程，由动量定理得：

I＝0－mv

解得挡板对滑块的冲量为：

I＝－m，负号表示方向向左.

(2)解法一　对小球下摆的过程，由动能定理得：

mgl+W＝mv

解得细绳对其做的功为：

W＝－mgl.

解法二　绳的张力对小球所做功的绝对值等于滑块在碰前的动能(或等于绳子的张力对滑块做的功)，则有：

W′＝mv或W′＝mv－0

解得：W＝－W′＝－mgl.

解法三　绳子的张力对小球做的功等于小球在全过程中的机械能的增量，取滑块所在高度的水平面为参考平面，有：

W＝(－mg·)－0＝－mgl(取水平位置为重力势能零点)

或W＝mgl(1－cos 60°)－mgl＝－mgl(取最低点为重力势能零点)

或W＝0－mg·＝－mgl(取小球运动到的最高点为重力势能零点).

解法四　对小球运动的全过程，由动能定理得：

W+mglcos 60°＝0或W+mg·＝0

解得：W＝－mgl.

解法五　考虑小球从水平位置到最低点的过程：

若滑块固定，绳子的张力对小球不做功，小球处于最低点时的速率v_球′＝(由mgl＝mv_球′²得到)

若滑块不固定，绳子的张力对小球做功，小球处于最低点时的速率v_球＝(v_球应由前面正确求得)

则绳子对小球做的功为：

W＝mv－mv_球′²＝－mgl.

答案：(1)－m，负号表示方向向左

(2)－mgl

12.如图甲所示，有一个竖直固定在地面的透气圆筒，筒中有一劲度系数为k的轻弹簧，其下端固定，上端连接一质量为m的薄滑块，圆筒内壁涂有一层新型智能材料--ER流体，它对滑块的阻力可调.起初，滑块静止，ER流体对其阻力为0，弹簧的长度为L.现有一质量也为m的物体从距地面2L处自由落下，与滑块碰撞后粘在一起向下运动.为保证滑块做匀减速运动，且下移距离为时速度减为0，ER流体对滑块的阻力须随滑块下移而变.试求(忽略空气阻力)：

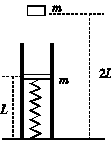(1)下落物体与滑块碰撞过程中系统损失的机械能.

(2)滑块向下运动过程中加速度的大小.

(3)滑块下移距离d时ER流体对滑块阻力的大小.

[2008年高考·重庆理综卷]

解析：(1)设物体自由下落的末速度为v₀，由机械能守恒定律有：

mgL＝mv

解得：v₀＝

设碰后共同速度为v₁，由动量守恒定律有：

2mv₁＝mv₀

解得：v₁＝

碰撞过程中系统损失的机械能为：

ΔE＝mv－×2mv＝mgL.

(2)设加速度的大小为a，有：2as＝v

解得：a＝.　　　　　　　　　　　　　　　　　　　　　　　　　 乙

(3)设弹簧的弹力为F_N，ER流体对滑块的阻力为F_ER，滑块的受力分析如图乙所示，则有：

F_N+F_ER－2mg＝2ma

F_N＝kx

x＝d+

解得：F_ER＝mg+－kd.

答案：(1)mgL　(2)　(3)mg+－kd.

11.总质量为80 kg的跳伞运动员从离地500 m的直升机上跳下，经过2 s拉开绳索开启降落伞，图示是跳伞过程中的v－t图，试根据图象求：(g取10 m/s²)

(1)t＝1 s时运动员的加速度和所受阻力的大小.

(2)估算14 s内运动员下落的高度及克服阻力做的功.

(3)估算运动员从飞机上跳下到着地的总时间.

[2008年高考·上海物理卷]

解析：(1)从图中可以看出，在t＝2 s内运动员做匀加速运动，其加速度大小为：

a＝＝ m/s²＝8 m/s²

设此过程中运动员受到的阻力大小为f，根据牛顿第二定律，有：mg－f＝ma

得：f＝m(g－a)＝80×(10－8) N＝160 N.

(2)从图中估算得出运动员在14 s内下落的高度为：

h＝40×2×2 m＝160 m

根据动能定理，有：mgh－W_f＝mv²

所以有：W_f＝mgh－mv²

＝(80×10×160－×80×6²) J

≈1.27×10⁵ J.

　(3)14 s后运动员做匀速运动的时间为：

t′＝＝ s＝57 s

故运动员从飞机上跳下到着地需要的总时间为：

t_总＝t+t′＝(14+57) s＝71 s.

答案：(1)8 m/s²　160 N

(2)160 m　1.27×10⁵ J　(3)71 s

10.运动员跳伞将经历加速下降和减速下降两个过程，将人和伞看成一个系统，在这两个过程中，下列说法正确的是[2008年高考·广东物理卷](　)

A.阻力对系统始终做负功

B.系统受到的合外力始终向下

C.重力做功使系统的重力势能增加

D.任意相等的时间内重力做的功相等

解析：在这两个过程中，阻力始终对系统做负功，选项A正确；加速下降时系统受到的合力向下，减速下降时系统受到的合力向上，选项B错误；这两个过程中，重力始终做正功，系统的重力势能减少，选项C错误；在任意相等的时间内，系统下降的高度不相等，故重力做的功不相等，选项D错误.

答案：A

9.一个25 kg的小孩从高度为3.0 m的滑梯顶端由静止开始滑下，滑到底端时的速度为2.0 m/s.取g＝10 m/s²，关于力对小孩做的功，以下结果正确的是[2008年高考·广东理科基础卷](　)

A.合外力做功50 J　 B.阻力做功500 J

C.重力做功500 J　 D.支持力做功50 J

解析：合外力做的功等于小孩动能的变化量，即W_合＝mgh+W_f＝ΔE_k＝50 J，选项A正确；重力做功750 J，阻力做功－700 J，支持力不做功，选项B、C、D错误.

答案：A

8.汽车沿一段坡面向下行驶，通过刹车使速度逐渐减小，在刹车过程中[2008年高考·广东文科基础卷](　)

A.重力势能增加　 B.动能增加

C.重力做负功　 D.机械能不守恒

解析：汽车向下行驶，高度在降低，重力势能在减小，选项A错误；汽车向下行驶，重力做正功，选项C错误；已知刹车时速度在减小，所以动能减小，选项B错误；刹车过程中，摩擦力做负功，产生热量，所以机械能减小，选项D正确.

答案：D

7.如图所示，一轻绳的一端系在固定粗糙斜面上的O点，另一端系一小球，给小球一足够大的初速度，使小球在斜面上做圆周运动.在此过程中[2008年高考·海南物理卷](　)

A.小球的机械能守恒

B.重力对小球不做功

C.绳的张力对小球不做功

D.在任何一段时间内，小球克服摩擦力所做的功总是等于小球动能的减少

解析：斜面粗糙，小球受到重力、支持力、摩擦力、绳子拉力，由于除重力做功外，摩擦力做负功，机械能减少，选项A、B错误；绳子张力总是与运动方向垂直，故不做功，选项C正确；小球动能的变化等于合外力做的功，即重力与摩擦力做的功，选项D错误.

答案：C

6.物体做自由落体运动，E_k代表动能，E_p代表势能，h代表下落的距离，以水平地面为零势能面.下列所示图象中，能正确反映各物理量之间关系的是[2008年高考·上海物理卷](　)

解析：由机械能守恒定律有E_p＝E－E_k，故E_p－E_k图象为倾斜的直线，选项C错误；

由动能定理有E_k＝mgh＝mv²＝mg²t²，则E_p＝E－mgh，故E_p－h图象也为倾斜的直线，选项D错误；又E_p＝E－mv²，故E_p－v图象为开口向下的抛物线，选项B正确；同理，E_p＝E－mg²t²，E_p－t图象也为开口向下的抛物线，选项A错误.

答案：B