6.如图甲所示，一薄木板放在正方形水平桌面上，木板的两端与桌面的两端对齐，一小木块放在木板的正中间.木块和木板的质量均为m，木块与木板之间、木板与桌面之间的动摩擦因数都为μ.现突然以一水平外力F将薄木板抽出，要使小木块不从桌面上掉下，则水平外力F至少应为多大？(假设木板抽动过程中始终保持水平，且在竖直方向上的压力全部作用在水平桌面上)

解析：方法一　F越大，木块与木板分离时的速度、位移越小，木块越不可能从桌面滑下.设当拉力为F0时，木块恰好能滑至桌面的边缘，再设木块与木板分离的时刻为t1，在0-t1时间内有：

··t－μgt＝

对t1时间后木块滑行的过程，有：

＝＝－μgt

解得：F0＝6μmg.

乙

方法二　F越大，木块与木板分离时的速度、位移越小，木块越不可能从桌面滑出.若木块不从桌面滑出，则其v－t 图象如图乙中OBC所示，其中OB的斜率为μg，BC的斜率为－μg，t1＝t2

有：S△OBC＝(·μgt)×2≤

设拉力为F时，木板的v－t图象为图乙中的直线OA，则S△OAB＝

即(v2－v1)·t1＝

其中v1＝μgt1，v2＝·t1

解得：F≥6μmg

即拉力至少为6μmg.

答案：6μmg

第17讲　牛顿运动定律的应用Ⅱ

体验成功

5.如图甲所示，滑块A置于光滑的水平面上，一细线的一端固定于倾角θ＝45°、质量为M的光滑楔形滑块A的顶端P处，细线另一端拴一质量为m的小球B.现对滑块施加一水平方向的恒力F，要使小球B能相对斜面静止，恒力F应满足什么条件？

解析：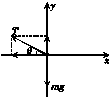

乙

先考虑恒力背离斜面方向(水平向左)的情况.设恒力大小为F1时，B还在斜面上且对斜面的压力为零，此时A、B有共同的加速度a1，B的受力情况如图乙所示，有：

Tsin θ＝mg，Tcos θ＝ma1

解得：a1＝gcot θ

即F1＝(M+m)a1＝(M+m)gcot θ

由此可知，当水平向左的力大于(M+m)gcot θ时，小球B将离开斜面.

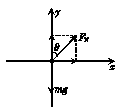对于水平恒力向斜面一侧方向(水平向右)的情况，设恒力大小为F2时，B相对斜面静止时对悬绳的拉力恰好为零，此时A、B的共同加速度为a2，

B的受力情况如图丙所示，有：FNcos θ＝mg，FNsin θ＝ma2

解得：a2＝gtan θ

即F2＝(M+m)a2

＝(M+m)gtan θ

由此可知，当水平向右的力大于(M+m)gtan θ，B将沿斜面上滑

综上可知，当作用在A上的恒力F向左小于(M+m)gcot θ，或向右小于(M+m)gtan θ时，B能静止在斜面上.

答案：向左小于(M+m)gcot θ或向右小于(M+m)gtan θ

4.如图所示，在水平桌面上叠放着质量均为M的A、B两块木板，在木板A的上面放着一个质量为m的物块C，木板和物块均处于静止状态.A、B、C之间以及B与地面之间的动摩擦因数都为μ.若用水平恒力F向右拉动木板A，使之从C、B之间抽出来，已知重力加速度为g，则拉力F的大小应该满足的条件是(已知最大静摩擦力的大小等于滑动摩擦力)(　)

A.F＞μ(2m+M)g　 B.F＞μ(m+2M)g

C.F＞2μ(m+M)g　 D.F＞2μmg

解析：无论F多大，摩擦力都不能使B向右滑动，而滑动摩擦力能使C产生的最大加速度为μg，故＞μg时，即F＞2μ(m+M)g时A可从B、C之间抽出.

答案：C

然后隔离重物利用牛顿第二定律可得：F′－mg＝ma

取立两式可得：F′＝F，故选项C正确.

答案：C

3.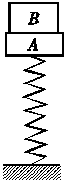如图所示，竖直放置在水平面上的轻弹簧上放着质量为2 kg的物体A，处于静止状态.若将一个质量为3 kg的物体B竖直向下轻放在A上的一瞬间，A对B的压力大小(取g＝10 m/s2)(　)

A.30 N　B.0　C.15 N　D.12 N

解析：刚放上的瞬间，取AB整体为研究对象：

(mA+mB)g－kx0＝(mA+mB)a

其中kx0＝mAg

取B为研究对象：mBg－FN＝mBa

解得：FN＝g＝12 N.

答案：D

19、已知盒中装有仅颜色不同的玻璃球6个，其中红球2个、黑球3个、白球1个.

(I)从中任取1个球, 求取得红球或黑球的概率；

(II)列出一次任取2个球的所有基本事件.

(III)从中取3个球，求至少有一个红球的概率.

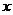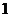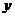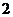18、先后随机投掷2枚正方体骰子，其中表示第枚骰子出现的点数，表示第枚骰子出现的点数。设点P的坐标为。　

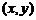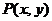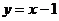(Ⅰ)求点在直线上的概率；

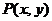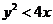(Ⅱ)求点满足的概率。

17、 　由经验得知，在某商场付款处排队等候付款的人数及概率如下表：

(1)至多有2人排队的概率是多少?　　

(2)至少有2人排队的概率是多少?

16、下列是容量为100的样本的频率分布直方图,

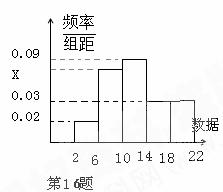试根据图形中的数据填空:

(1)样本数据落在范围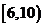内的频率为　 。

(2)样本数据落在范围内的频数为　 。 　

(3) 样本数据落在范围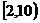的概率约为　　　　 。　

15、邵阳市二中高一学生李明放学回家坐8路车，8路车每5分钟一班，问李明等车时间不超过3分钟的概率是　　　　 。

14、右图给出的是计算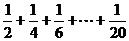的值的

一个流程图，其中判断框内应填入的条件

是　　 　　　　　 　。