20．(12分)某渔业公司年初用98万元购买一艘捕鱼船，第一年各种费用为12万元，以后每年都增加4万元，每年捕鱼收益50万元．

(1)问第几年开始获利?

　(2)若干年后，有两种处理方案：

　方案一：年平均获利最大时，以26万元出售该渔船

　方案二：总纯收入获利最大时，以8万元出售该渔船．问哪种方案合算．

18．(12分)在一次由三人参加的围棋对抗赛中，甲胜乙的概率为0.4，乙胜丙的概率为0.5，丙胜甲的概率为0.6，比赛按以下规则进行；第一局：甲对乙；第二局：第一局胜者对丙；第三局：第二局胜者对第一局败者；第四局：第三局胜者对第二局败者，求：

(1)乙连胜四局的概率；

(2)丙连胜三局的概率．

　注意：考生在(19甲)、(19乙)两题中选一题作答，如果两题都答，只以(19甲)计分．

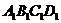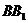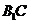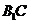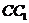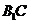　19甲．(12分)已知长方体ABCD-中，棱AB＝BC＝3，＝4，连结，过B点作的垂线交于E，交于F．

　(1)求证：⊥平面EBD；

　(2)求ED与平面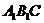所成角的大小；

　(3)求二面角E-BD-C的大小．

　19乙．(12分)如图，在正方体ABCD-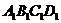中，E、F分别是，CD的中点．

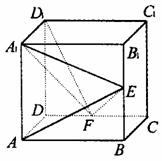　(1)证明：AD⊥；

　(2)求AE与所成的角；

　(3)证明：面AED⊥面；

　(4)设＝2，求三棱锥F-的体积．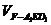

17．(12分)已知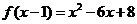，，3]．

(1)求f(x)；

　(2)求；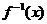

　(3)在f(x)与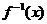的公共定义域上，解不等式f(x)＞+．

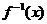16．连结双曲线与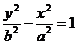(a＞0，b＞0)的四个顶点的四边形面积为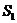，连结四个焦点的四边形的面积为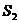，则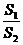的最大值是________．

15．设向量a＝(cos23°，cos67°)，b＝(cos68°，cos22°)，u＝a+tb()则|u|的最小值是________．

14．如图，空间有两个正方形ABCD和ADEF，M、N分别在BD、AE上，有BM＝AN，那么

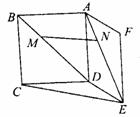
　①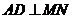；②MN∥平面CDE；③MN∥CE；④MN、CE是异面直线．

　以上四个结论中，不正确的是________．

13．已知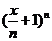展开式中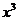项的系数是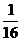，则正整数n＝________．

12．已知函数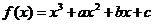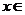，[-2，2]表示的曲线过原点，且在x＝±1处的切线斜率均为-1，有以下命题：

　①f(x)的解析式为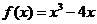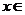：，[-2，2]　②f(x)的极值点有且仅有一个

　③f(x)的最大值与最小值之和等于零　其中正确的命题个数为(　)

　A．0个　　 B．1个　　 C．2个　　 D．3个

第Ⅱ卷(非选择题，共90分)

11．以三角形的三个顶点和它内部的三个点共6个点为顶点，能把原三角形分割成的小三角形的个数是(　)

　A．9　　　 B．8　　　C．7　　　D．6

10．如图，正三棱锥A-BCD中，E在棱AB上，F在棱CD上．并且(0＜l＜+∞)，设a 为异面直线EF与AC所成的角，b 为异面直线EF与BD所成的角，则a+b 的值是(　)

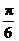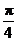　A．　　B．　C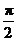．　　D．与l 有关的变量