18、(本大题满分16分)

解：(1)由题意,得,即,解得……3分

(2)

　=

(3)①当时,因为,所以当时,有最小值12100

②当时,∵在上递减,∴当时,有最小值12400

∵12100〈12400，∴当时，该商品的日销售金额取得最小值为12100

17、(本大题满分14分)

解：(1)当，　 ………………2分

令

因此　 …………6分

　 (2)

………………8分

令。

①若

由；　 ………………12分

②若

由；　 ………………16分

综上，

16、(本大题满分14分)

解：(1)因为，所以，

即，所以，

所以．

　(2)因为 ，所以，所以，，

　又点在角的终边上，所以， ．

同理 ，，

所以．

15、(本大题满分14分)

解：(Ⅰ)设等差数列的公差。

　　　　 因为

　　　　 所以　　　 解得

所以

　 (Ⅱ)设等比数列的公比为

　　　　 因为

所以　 即=3

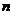所以的前项和公式为

20．已知二次函数．

(1)若，试判断函数零点个数；

(2)若对且，，试证明，使

成立；

(3)是否存在，使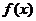同时满足以下条件①对，

，且；②对,都有

．若存在，求出的值，若不存在，请说明理由．

19．已知函数().

(I)若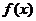的定义域和值域均是，求实数的值；

(II)若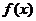在区间上是减函数，且对任意的，，总有，求实数的取值范围.

18．经市场调查，某商场的一种商品在过去的一个月内(以30天计)销售价格(元)与时间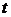(天)的函数关系近似满足(为正常数)，日销售量(件)与时间(天)的函数关系近似满足，且第25天的销售金额为13000元.

(1)求的值；

(2)试写出该商品的日销售金额关于时间的函数关系式；

(3)该商品的日销售金额的最小值是多少？.

17．已知．

(1)若的单调递增区间；

(2)若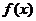的最大值为3，求实数m的值．

16．在平面直角坐标系中，点在角的终边上，点在角的终边上，且．

(1)求的值；(2)求．

15．已知数列为等差数列，且，．

(1)求的通项公式；

(2)若等比数列满足，，求的前n项和公式．