
1.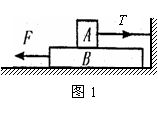 如图1所示,木板B放在粗糙水平面上,木块A放在B的上面,A的右端通过一不可伸长的轻绳固定在竖直墙上,用水平恒力F向左拉动B,使其以速度v做匀速运动,此时绳水平且拉力大小为T,下面说法正确的是( )
如图1所示,木板B放在粗糙水平面上,木块A放在B的上面,A的右端通过一不可伸长的轻绳固定在竖直墙上,用水平恒力F向左拉动B,使其以速度v做匀速运动,此时绳水平且拉力大小为T,下面说法正确的是( )
A.绳上拉力T与水平恒力F大小相等
B.木块A受到的是静摩擦力,大小等于T
C.木板B受到一个静摩擦力,一个滑动摩擦力,合力大小等于F 
D.若木板B以2v匀速运动,则拉力仍为F
21. (本题满分14分)
(理)已知数列满足: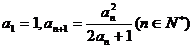 ,
,
(1).求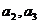 的值。
的值。
(2)求数列的通项公式。
(3)求证: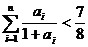
(文)设数列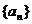 的前
的前 项和为
项和为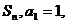 且对任意正整数
且对任意正整数 ,点
,点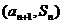 在直线
在直线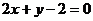 上.
上.
(1)求数列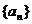 的通项公式;
的通项公式;
(2)是否存在实数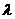 ,使得数列
,使得数列 为等差数列?若存在,求出
为等差数列?若存在,求出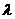 的值,若不存在,则说明理由;
的值,若不存在,则说明理由;
(3)设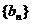 满足:
满足: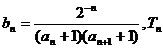 为数列
为数列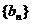 的前
的前 项和,求证:
项和,求证: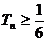
20. (本题满分13分)
已知函数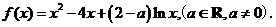
(1)当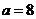 时,求函数
时,求函数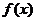 的单调区间;
的单调区间;
(2)求函数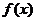 在区间
在区间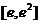 上的最小值.
上的最小值.
19. (本题满分12分)
设函数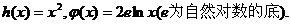
(1) 求函数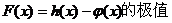 ;
;
(2) 若存在常数k和b,使得函数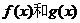 对其定义域内的任意实数
对其定义域内的任意实数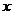 分别满足
分别满足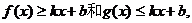 则称直线
则称直线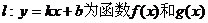 的“隔离直 线”.试问:函数
的“隔离直 线”.试问:函数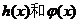 是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由.
是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由.
18. (本题满分12分)
某林场原有木材存有量为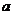 立方米,又木材以每年
立方米,又木材以每年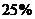 的增长率增长,而年终又要砍伐的木材量为
的增长率增长,而年终又要砍伐的木材量为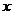 立方米,为了实现经过20年达到木材量至少翻两番的目标,则
立方米,为了实现经过20年达到木材量至少翻两番的目标,则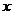 的最大值是多少?(
的最大值是多少?(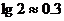 )
)
17. (本题满分12分)
(理)在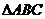 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为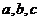 ,且满足
,且满足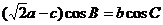 .
.
(1)求角B的大小;
(2)设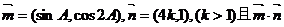 的最大值是7,求k的值。
的最大值是7,求k的值。
(文)已知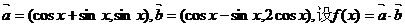 。
。
(1)求函数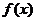 的最小正周期;
的最小正周期;
(2)当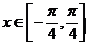 时,求函数
时,求函数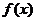 的最大值,并指出此时x的值。
的最大值,并指出此时x的值。
16. (本题满分12分)
设集合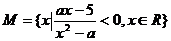 .
.
(1) 当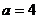 时,化简集合
时,化简集合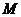 ;
;
(2)若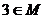 ,且
,且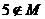 ,求实数
,求实数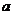 的取值范围.
的取值范围.
15.已知数列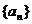 中,
中,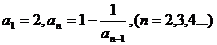 ,则
,则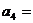 ;若数列
;若数列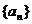 有一形如
有一形如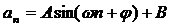 的通项公式,其中
的通项公式,其中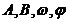 均为实数,且
均为实数,且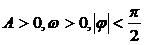 ,则此数列的通项公式可以为
,则此数列的通项公式可以为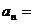 (写出一个即可).
(写出一个即可).
14.给出下列命题:
(1)若实数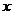 满足
满足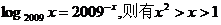 成立;
成立; 
(2)若 则不等式
则不等式 恒成立;
恒成立;
(3)对于函数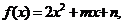 若
若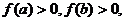 则函数在
则函数在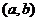 内至多有一零点;
内至多有一零点;
(4)函数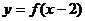 与
与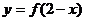 的图像关于直线
的图像关于直线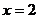 对称;
对称;
则其中所有正确命题的序号是 .
13.(理)函数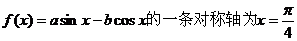 ,则直线
,则直线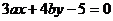 的斜率为
的斜率为

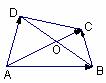 (文)如图,四边形ABCD中,设
(文)如图,四边形ABCD中,设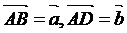 ,对角线AC与BD交于点O,若点O为BD的中点,且
,对角线AC与BD交于点O,若点O为BD的中点,且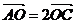 ,则
,则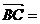 ;(用
;(用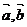 表示)
表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com