
1、 下列关于所描述的运动中,可能的是 ( )
A 速度变化很大,加速度很小
B 速度变化的方向为正,加速度方向为负
C 速度变化越来越快,加速度越来越小
D 速度越来越大,加速度越来越小
解析:由a=△v/△t知,即使△v很大,如果△t足够长,a可以很小,故A正确。速度变化的方向即△v的方向,与a方向一定相同,故B错。加速度是描述速度变化快慢的物理量,速度变化快,加速度一定大。故C错。加速度的大小在数值上等于单位时间内速度的改变量,与速度大小无关,故D正确。
答案:A、D
例题1.一物体做匀变速直线运动,某时刻速度大小为4m/s,1s后速度的大小变为10m/s,在这1s内该物体的 ( )
A.位移的大小可能小于4m
B.位移的大小可能大于10m
C.加速度的大小可能小于4m/s
D.加速度的大小可能大于10m/s
析:同向时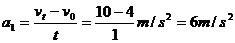
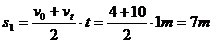
反向时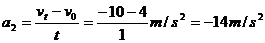
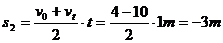
式中负号表示方向跟规定正方向相反
答案:A、D
例题2:两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木快每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知 ( )
A 在时刻t2以及时刻t5两木块速度相同
B 在时刻t1两木块速度相同
C 在时刻t3和时刻t4之间某瞬间两木块速度相同
D 在时刻t4和时刻t5之间某瞬间两木块速度相同
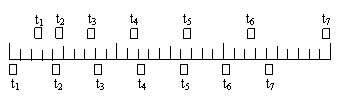 解析:首先由图看出:上边那个物体相邻相等时间内的位移之差为恒量,可以判定其做匀变速直线运动;下边那个物体很明显地是做匀速直线运动。由于t2及t3时刻两物体位置相同,说明这段时间内它们的位移相等,因此其中间时刻的即时速度相等,这个中间时刻显然在t3、t4之间
解析:首先由图看出:上边那个物体相邻相等时间内的位移之差为恒量,可以判定其做匀变速直线运动;下边那个物体很明显地是做匀速直线运动。由于t2及t3时刻两物体位置相同,说明这段时间内它们的位移相等,因此其中间时刻的即时速度相等,这个中间时刻显然在t3、t4之间
答案:C
例题3 一跳水运动员从离水面10m高的平台上跃起,举双臂直立身体离开台面,此时中心位于从手到脚全长的中点,跃起后重心升高0.45m达到最高点,落水时身体竖直,手先入水(在此过程中运动员水平方向的运动忽略不计)从离开跳台到手触水面,他可用于完成空中动作的时间是多少?(g取10m/s2结果保留两位数字)
解析:根据题意计算时,可以把运动员的全部质量集中在重心的一个质点,且忽略其水平方向的运动,因此运动员做的是竖直上抛运动,由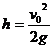 可求出刚离开台面时的速度
可求出刚离开台面时的速度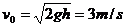 ,由题意知整个过程运动员的位移为-10m(以向上为正方向),由
,由题意知整个过程运动员的位移为-10m(以向上为正方向),由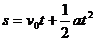 得:
得:
-10=3t-5t2
解得:t≈1.7s
思考:把整个过程分为上升阶段和下降阶段来解,可以吗?
 例题4.如图所示,有若干相同的小钢球,从斜面上的某一位置每隔0.1s释放一颗,在连续释放若干颗钢球后对斜面上正在滚动的若干小球摄下照片如图,测得AB=15cm,BC=20cm,试求:
例题4.如图所示,有若干相同的小钢球,从斜面上的某一位置每隔0.1s释放一颗,在连续释放若干颗钢球后对斜面上正在滚动的若干小球摄下照片如图,测得AB=15cm,BC=20cm,试求:
(1) 拍照时B球的速度;
(2) A球上面还有几颗正在滚动的钢球
解析:拍摄得到的小球的照片中,A、B、C、D…各小球的位置,正是首先释放的某球每隔0.1s所在的位置.这样就把本题转换成一个物体在斜面上做初速度为零的匀加速运动的问题了。求拍摄时B球的速度就是求首先释放的那个球运动到B处的速度;求A球上面还有几个正在滚动的小球变换为首先释放的那个小球运动到A处经过了几个时间间隔(0.1s)
(1)A、B、C、D四个小球的运动时间相差△T=0.1s
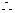 VB=
VB=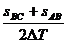 =
= m/s=1.75m/s
m/s=1.75m/s
(2)由△s=a△T2得:
a=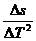 m/s2=
m/s2=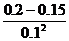 =5m/s2
=5m/s2
例5:火车A以速度v1匀速行驶,司机发现正前方同一轨道上相距s处有另一火车B沿同方向以速度v2(对地,且v2〈v1〉做匀速运动,A车司机立即以加速度(绝对值)a紧急刹车,为使两车不相撞,a应满足什么条件?
分析:后车刹车做匀减速运动,当后车运动到与前车车尾即将相遇时,如后车车速已降到等于甚至小于前车车速,则两车就不会相撞,故取s后=s+s前和v后≤v前求解
解法一:取取上述分析过程的临界状态,则有
v1t-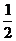 a0t2=s+v2t
a0t2=s+v2t
v1-a0t = v2
a0 =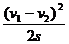
所以当a≥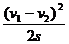 时,两车便不会相撞。
时,两车便不会相撞。
法二:如果后车追上前车恰好发生相撞,则
v1t-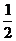 at2 = s +v2t
at2 = s +v2t
上式整理后可写成有关t的一元二次方程,即
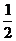 at2+(v2-v1)t+s = 0
at2+(v2-v1)t+s = 0
取判别式△〈0,则t无实数解,即不存在发生两车相撞时间t。△≥0,则有
(v2-v1)2≥4(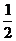 a)s
a)s
得a≤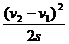
 为避免两车相撞,故a≥
为避免两车相撞,故a≥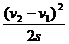
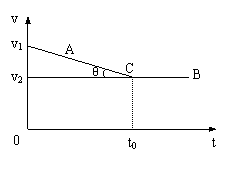
法三:运用v-t图象进行分析,设从某时刻起后车开始以绝对值为a的加速度开始刹车,取该时刻为t=0,则A、B两车的v-t图线如图所示。图中由v1 、v2、C三点组成的三角形面积值即为A、B两车位移之差(s后-s前)=s,tanθ即为后车A减速的加速度绝对值a0。因此有
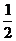 (v1-v2)
(v1-v2)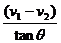 =s
=s
所以 tanθ=a0=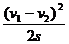
若两车不相撞需a≥a0=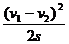
22.(14分)已知向量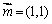 ,向量
,向量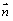 与向量
与向量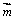 夹角为
夹角为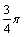 ,且
,且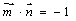 .
.
(1)求向量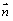 ;
;
(2)若向量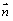 与向量
与向量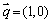 的夹角为
的夹角为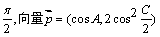 ,其中
,其中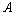 ,
,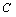 为
为
△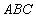 的内角,且
的内角,且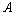 ,
,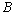 ,
,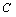 依次成等差数列,试求|
依次成等差数列,试求|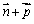 |的取值范围.
|的取值范围.
21.(12分)某工厂生产A、B两类型桌子,每张桌子需木工和油漆两道工序完成。已知木工做A、B型桌子各一张分别需要1小时和2小时;漆工油漆A、B型桌子各一张分别需要3小时和1小时;又知木工、漆工每天工作时间分别不得得超过8小时和9小时,而生产一张A、B型桌子的利润分别为15元和20元,试问工厂每天应生产A、B型桌子各多少张,才能获得最大利润最大?最大利润是多少?
20.(12分)已知数列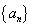 中,
中,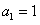 ,点
,点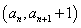 在函数
在函数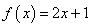 的图像上。
的图像上。
(1)求数列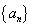 的通项公式; (2)求数列
的通项公式; (2)求数列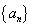 的前n项和
的前n项和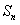 ;
;
(3)设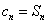 ,求数列
,求数列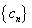 的前n项和
的前n项和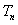 。
。
19.(12分)已知f(x)=x3+ax2+bx+c,在x=1与x=-2时,都取得极值。
⑴求a,b的值;
⑵若x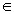 [-3,2]都有f(x)>
[-3,2]都有f(x)>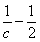 恒成立,求c的取值范围。
恒成立,求c的取值范围。
18. (12分)已知集合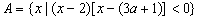 ,
,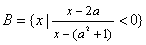 .
.
(1)当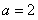 时,求
时,求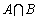 ;
;
(2)求使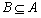 的实数
的实数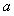 的取值范围.
的取值范围.
17. (12分)已知: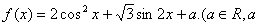 为常数)
为常数)
(1)若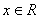 ,求
,求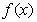 的最小正周期;
的最小正周期;
(2)若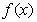 在
在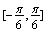 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求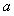 的值;
的值;
(3)在(2)条件下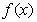 经过怎样的变换后得到
经过怎样的变换后得到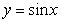 ,写出其变换步骤.
,写出其变换步骤.
16.设函数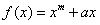 的导数为
的导数为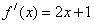 ,则数列
,则数列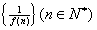 的前
的前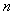 项和是
项和是
15.若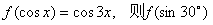 =_______________
.
=_______________
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com