1、有关P、Q两地的说法正确的是(　)

A．P地地势、降水量均高于Q地

B．P地降水多于Q地，气温低于Q地

C．P、Q两地海拔高度相同，气温相同

D．Q地具有较明显的热岛效应和雨岛效应

21、(本小题满分14分)

　设不等式组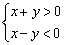表示的平面区域为D，区域内的动点P到直线l₁：x+y=0和直线l₂：x－y=0的距离之积为2，记点P的轨迹为曲线T．

　(Ⅰ)求曲线T的方程；

　(Ⅱ)过点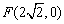的直线l与曲线T交于A，B两点，求直线l的斜率k的取值范围，若以AB为直径的圆与y轴相切，求k的值．

20、(本小题满分13分)已知函数．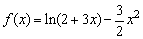

　(Ⅰ)求f(x)在[0，1]上的极值；

　(Ⅱ)若关于x的方程f(x)=－2x+b在[0，1]上恰有两个不同的实根，求实数b的取值范围．

19、(本小题满分12分)如图，平面四边形ABCD中，AB=13，三角形ABC的面积为S_△ABC=25，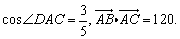

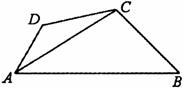求：(1)BC的长；

(2)cos∠BAD的值．

18、(本小题满分12分)已知数列{a_n}的前n项和为S_n，点(a_n+2，S_n+1)在直线y=4x－5上，其中n∈N^*．令b_n=a_n+1－2a_n，且a₁=1．

(1)求数列{b_n}的通项公式；

(2)若f(x)=b₁x+b₂x²+b₃x³+…+b_nxⁿ，求f′(1)的表达式．

17、(本小题满分12分)射击运动员在双向飞碟射击比赛中，每轮比赛连续发射两枪，击中两个飞靶得2分，击中一个得1分，未击中0分．某运动员在每轮比赛时，第一枪命中率为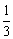，第二枪命中率为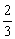，该运动员只进行两轮比赛．

求：(1)求该运动员得4分的概率；

(2)若该运动员所得分数为ξ，求ξ的分布列及数学期望．

16、(本小题满分12分)

　已知θ是△ABC的最大的内角．设向量a=(cosθ，sinθ)，b=(sin2θ，1－cos2θ)，c=(0，－1)．定义f(θ)=(a+b)¡c+|b|，求f(θ)的最大值．

15、定义域和值域均为[－a，a](常数a＞0)的函数y=f(x)和y=g(x)的图像如图所示，给出下列四个命题：

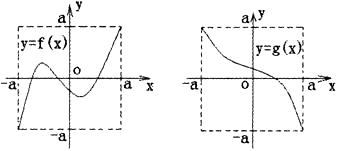
(1)方程f[g(x)]=0有且仅有三个解；

(2)方程g[f(x)]=0有且仅有三个解；

(3)方程f[f(x)]=0有且仅有九个解；

(4)方程g[g(x)]=0有且仅有一个解．

那么，其中所有正确命题的序号是__________．

14、已知函数f(x)的导函数为f′(x)，且满足f(x)=3x²+2xf′(2)，则f′(5)=__________．

13、在闭区间[－1，1]上任取两个实数，则它们的和不大于1的概率是__________．