
6.2009年山东(文21)(本小题满分12分)
已知函数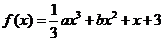 ,其中
,其中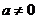
(1)
当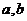 满足什么条件时,
满足什么条件时, 取得极值?
取得极值?
(2)
已知 ,且
,且 在区间
在区间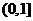 上单调递增,试用
上单调递增,试用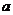 表示出
表示出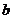 的取值范围.
的取值范围.
解: (1)由已知得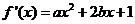 ,令
,令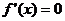 ,得
,得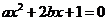 ,
,
 要取得极值,方程
要取得极值,方程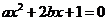 必须有解,
必须有解,
所以△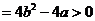 ,即
,即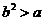 ,
此时方程
,
此时方程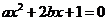 的根为
的根为
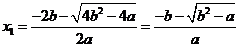 ,
,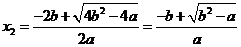 ,
,
所以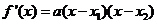
当 时,
时,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当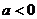 时,
时,
|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
f’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
所以 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当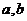 满足
满足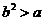 时,
时,  取得极值.
取得极值.
(2)要使 在区间
在区间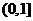 上单调递增,需使
上单调递增,需使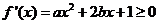 在
在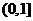 上恒成立.
上恒成立.
即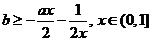 恒成立, 所以
恒成立, 所以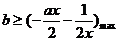
设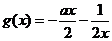 ,
,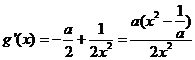 ,
,
令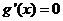 得
得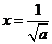 或
或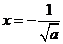 (舍去),
(舍去),
当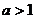 时,
时,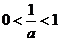 ,当
,当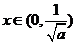 时
时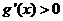 ,
,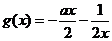 单调增函数;
单调增函数;
当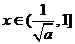 时
时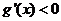 ,
,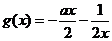 单调减函数,
单调减函数,
所以当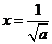 时,
时,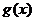 取得最大,最大值为
取得最大,最大值为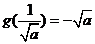 . 所以
. 所以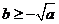
当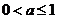 时,
时, ,此时
,此时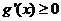 在区间
在区间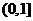 恒成立,所以
恒成立,所以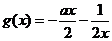 在区间
在区间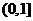 上单调递增,当
上单调递增,当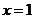 时
时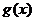 最大,最大值为
最大,最大值为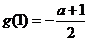 ,所以
,所以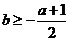
综上,当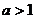 时,
时, 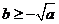 ; 当
; 当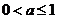 时,
时, 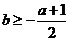
分析::本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
21. 解法一:(1)如图,由题意知AC⊥BC,
解法一:(1)如图,由题意知AC⊥BC,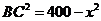 ,
,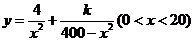
其中当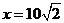 时,y=0.065,所以k=9
时,y=0.065,所以k=9
所以y表示成x的函数为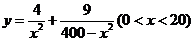
(2)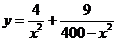 ,
,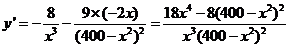 ,令
,令 得
得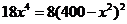 ,所以
,所以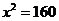 ,即
,即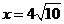 ,当
,当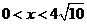 时,
时, 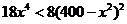 ,即
,即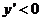 所以函数为单调减函数,当
所以函数为单调减函数,当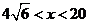 时,
时, 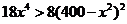 ,即
,即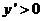 所以函数为单调增函数.所以当
所以函数为单调增函数.所以当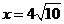 时, 即当C点到城A的距离为
时, 即当C点到城A的距离为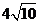 时, 函数
时, 函数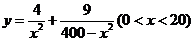 有最小值.
有最小值.
解法二: (1)同上.
(2)设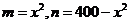 ,则
,则 ,
, ,
,
所以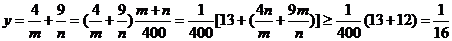
当且仅当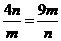 即
即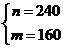 时取”=”.
时取”=”.
下面证明函数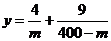 在(0,160)上为减函数, 在(160,400)上为增函数.
在(0,160)上为减函数, 在(160,400)上为增函数.
设0<m1<m2<160,则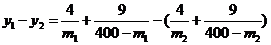
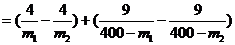
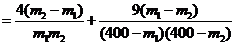
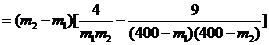
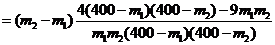 ,
,
因为0<m1<m2<160,所以4 >4×240×240
>4×240×240
9 m1m2<9×160×160所以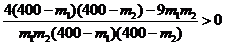 ,
,
所以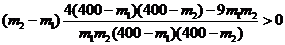 即
即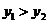 函数
函数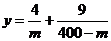 在(0,160)上为减函数.
在(0,160)上为减函数.
同理,函数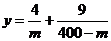 在(160,400)上为增函数,设
在(160,400)上为增函数,设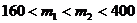 ,则
,则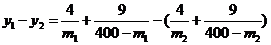
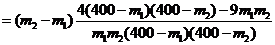
因为1600<m1<m2<400,所以4 <4×240×240, 9
m1m2>9×160×160
<4×240×240, 9
m1m2>9×160×160
所以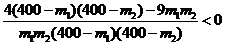 ,
,
所以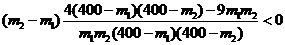 即
即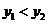 函数
函数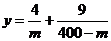 在(160,400)上为增函数.所以当m=160即
在(160,400)上为增函数.所以当m=160即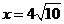 时取”=”,函数y有最小值,
时取”=”,函数y有最小值,
即弧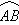 上存在一点,
上存在一点,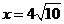 时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
分析:本题主要考查了函数在实际问题中的应用,运用待定系数法求解函数解析式的能力和运用换元法和基本不等式研究函数的单调性等问题.
5.2009年(山东理21)(本小题满分12分)
两县城A和B相距20Km,现计划在两县城外以AB为直径的半圆弧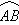 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和。记C点到城A的距离
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和。记C点到城A的距离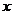 Km,建在C处的垃圾处理厂对城B的影响度为
Km,建在C处的垃圾处理厂对城B的影响度为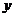 ,统计调查表明;垃圾处理厂对城A的影响度与所选地点到城B的平方成反比,比例系数为4;城B的影响度与所选地点到城B的距离的平方成反比,比例系数为K,当垃圾处理厂建在弧
,统计调查表明;垃圾处理厂对城A的影响度与所选地点到城B的平方成反比,比例系数为4;城B的影响度与所选地点到城B的距离的平方成反比,比例系数为K,当垃圾处理厂建在弧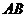 的中点时,对城A和城B)总影响度为0.065
的中点时,对城A和城B)总影响度为0.065
(Ⅰ)将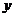 表示成
表示成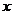 的函数;
的函数;
(Ⅱ)讨论(Ⅰ)中函数的单调性,并判断弧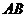 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点城A的距离;若不存在,说明理由。
3.2008山东卷理(21)(满分12分)
已知函数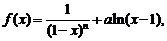 其中n∈N*,a为常数.
其中n∈N*,a为常数.
(Ⅰ)当n=2时,求函数f(x)的极值;
(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
(Ⅰ)解:由已知得函数f(x)的定义域为{x|x>1},
当n=2时,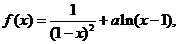
所以 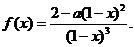
(1)当a>0时,由f(x)=0得 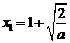 >1,
>1,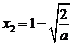 <1,
<1,
此时 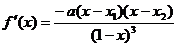 .
.
当x∈(1,x1)时,f′(x)<0,f(x)单调递减;
当x∈(x1+∞)时,f′(x)>0, f(x)单调递增.
(2)当a≤0时,f′(x)<0恒成立,所以f(x)无极值.
综上所述,n=2时,
当a>0时,f(x)在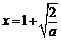 处取得极小值,极小值为
处取得极小值,极小值为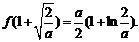
当a≤0时,f(x)无极值.
(Ⅱ)证法一:因为a=1,所以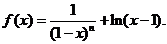
当n为偶数时,令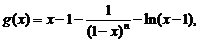
则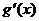 =1+
=1+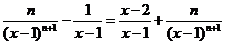 >0(x≥2).
>0(x≥2).
所以当x∈[2,+∞]时,g(x)单调递增, 又g(2)=0
因此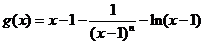 ≥g(2)=0恒成立,
≥g(2)=0恒成立,
所以f(x)≤x-1成立.
当n为奇数时,
要证 ≤x-1,由于
≤x-1,由于 <0,所以只需证ln(x-1) ≤x-1,
<0,所以只需证ln(x-1) ≤x-1,
令
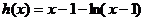 则
则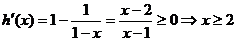
所以 当x∈[2,+∞]时,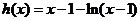 单调递增,又h(2)=1>0,
单调递增,又h(2)=1>0,
所以当x≥2时,恒有h(x) >0,即ln(x-1)<x-1命题成立.
综上所述,结论成立.
证法二:当a=1时,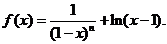
当x≤2,时,对任意的正整数n,恒有 ≤1,
≤1,
故只需证明1+ln(x-1) ≤x-1.
令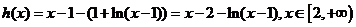
则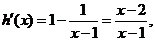
当x≥2时,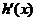 ≥0,故h(x)在
≥0,故h(x)在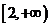 上单调递增,
上单调递增,
因此 当x≥2时,h(x)≥h(2)=0,即1+ln(x-1) ≤x-1成立.
故 当x≥2时,有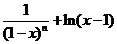 ≤x-1.即f(x)≤x-1.
≤x-1.即f(x)≤x-1.
分析:考查函数的导数概念、求导的技能和导数的应用。利用导数的工具研究函数的性质,不仅体现教材改革的一种理念,也是初等数学和高等数学一个很好的衔接点,该题解法中应用到函数与方程的思想,分类讨论、转化与化归思想,达到了知识内容考查与 思想方法考查相结合的目的。
4 2008年山东卷文 21.(满分12分)
设函数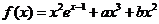 ,已知
,已知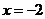 和
和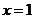 为
为 的极值点.
的极值点.
(Ⅰ)求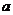 和
和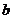 的值;(Ⅱ)讨论
的值;(Ⅱ)讨论 的单调性;
的单调性;
(Ⅲ)设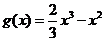 ,试比较
,试比较 与
与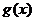 的大小.
的大小.
解:(Ⅰ)因为
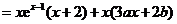 ,
,
又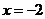 和
和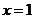 为
为 的极值点,所以
的极值点,所以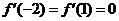 ,
,
因此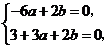 解方程组得
解方程组得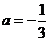 ,
,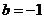 .
.
(Ⅱ)因为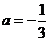 ,
,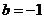 ,
,
所以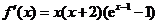 ,令
,令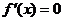 ,解得
,解得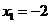 ,
,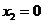 ,
,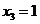 .
.
因为当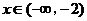
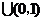 时,
时,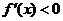 ; 当
; 当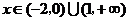 时,
时,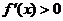 .
.
所以 在
在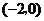 和
和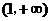 上是单调递增的;在
上是单调递增的;在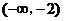 和
和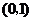 上是单调递减的.
上是单调递减的.
(Ⅲ)由(Ⅰ)可知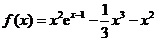 ,
,
故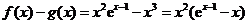 ,令
,令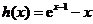 ,
,
则 . 令
. 令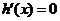 ,得
,得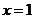 ,
,
因为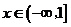 时,
时,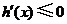 , 所以
, 所以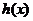 在
在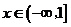 上单调递减.
上单调递减.
故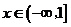 时,
时,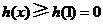 ; 因为
; 因为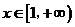 时,
时,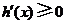 ,
,
所以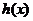 在
在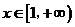 上单调递增. 故
上单调递增. 故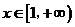 时,
时,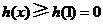 .
.
所以对任意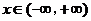 ,恒有
,恒有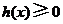 ,又
,又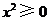 ,
,
因此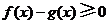 ,故对任意
,故对任意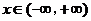 ,恒有
,恒有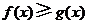 .
.
分析:考查函数的导数概念、求导的技能和导数的应用,求导后判断单调性和极值点时用到了方程的思想,与理科比较,题目虽简单,也达到了知识内容考查与 思想方法考查相结合的目的。
2.2008山东卷理(14)(满分4分)设函数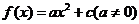 .若
.若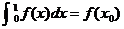 ,0≤x0≤1,则x0的值为 .
,0≤x0≤1,则x0的值为 .
解析:本题考查微积分定理的应用,题目虽简单,应注意本节常见题型。
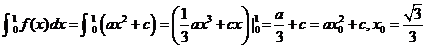
1.2007年山东卷理(22)(满分14分)设函数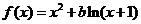 ,其中
,其中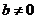 .
.
(I)当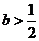 时,判断函数
时,判断函数 在定义域上的单调性; (II)求函数
在定义域上的单调性; (II)求函数 的极值点;
的极值点;
(III)证明对任意的正整数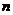 ,不等式
,不等式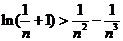 都成立.
都成立.
解:(I) 函数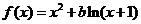 的定义域为
的定义域为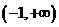 .
.
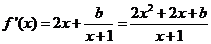 ,
,
令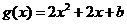 ,则
,则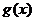 在
在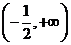 上递增,在
上递增,在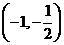 上递减,
上递减,
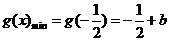 . 当
. 当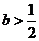 时,
时,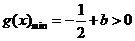 ,
,
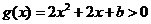 在
在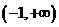 上恒成立.
上恒成立.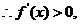
即当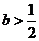 时,函数
时,函数 在定义域
在定义域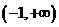 上单调递增。
上单调递增。
(II)分以下几种情形讨论:
(1)由(I)知当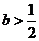 时函数
时函数 无极值点.
无极值点.
(2)当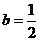 时,
时,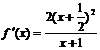 ,
,
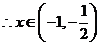 时,
时,
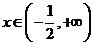 时,
时,
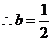 时,函数
时,函数 在
在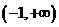 上无极值点。
上无极值点。
(3)当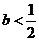 时,解
时,解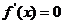 得两个不同解
得两个不同解
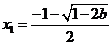 ,
,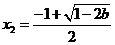 .
.
当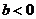 时,
时,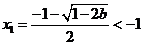 ,
,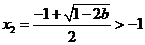 ,
,
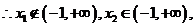
此时 在
在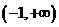 上有唯一的极小值点
上有唯一的极小值点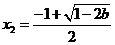 .
.
当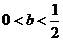 时,
时,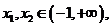
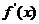 在
在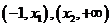 都大于0 ,
都大于0 ,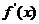 在
在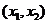 上小于0 ,
上小于0 ,
此时 有一个极大值点
有一个极大值点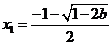 和一个极小值点
和一个极小值点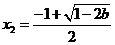 .
.
综上可知,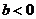 时,
时, 在
在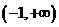 上有唯一的极小值点
上有唯一的极小值点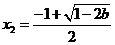 ;
;
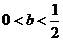 时,
时, 有一个极大值点
有一个极大值点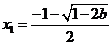 和一个极小值点
和一个极小值点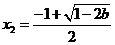 ;
;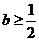 时,函数
时,函数 在
在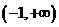 上无极值点。
上无极值点。
(III) 当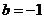 时,
时,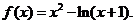
令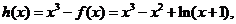
则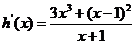 在
在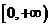 上恒正,
上恒正,
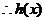 在
在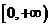 上单调递增,当
上单调递增,当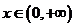 时,恒有
时,恒有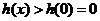 .
.
即当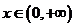 时,有
时,有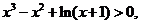
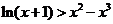 ,
,
对任意正整数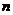 ,取
,取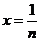 得
得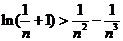
分析:考查导数有关的概念、计算和应用.利用导数工具研究函数的有关性质,把导数应用于单调性、极值等传统、常规问题的同时,进一步升华到处理与自然数 有关的不等式的证明,是函数知识和不等式知识的一个结合体,它的解题却融合了转化、分类讨论、函数与方程、数形结合等数学思想与方法,不但突出了能力的考查,这一切对考查考生的应用能力和创新意识都大有益处,又有针对参数的取值对函数单调区间及对函数的极值产生影响的讨论,该题达到了知识内容考查与思想方法考查相结合的目的。
4. 本单元的典型试题类型及解题方法、策略。
3. 本单元的考纲要求、复习措施:
考纲要求: (1)了解导数的概念,能利用导数定义求导数.掌握函数在一点处的导数的定义和导数的几何意义,理解导函数的概念.了解曲线的切线的概念.在了解瞬时速度的基础上抽象出变化率的概念. (2)熟记基本导数公式。掌握两个函数四则运算的求导法则和复合函数的求导法则,会求某些简单函数的导数,利能够用导数求单调区间,求一个函数的最大(小)值的问题,掌握导数的基本应用. (3)了解函数的和、差、积的求导法则的推导,掌握两个函数的商的求导法则。能正确运用函数的和、差、积的求导法则及已有的导数公式求某些简单函数的导数。 (4)了解复合函数的概念(理科)。会将一个函数的复合过程进行分解或将几个函数进行复合。掌握复合函数的求导法则,并会用法则解决一些简单问题。,
导数是新教材增加的内容,近几年的高考试题逐步加深.有关导数的高考题主要考查导数的几何意义、函数的单调性、极值,应用问题中的最值.由于导数的工具性,好多问题用导数处理显得简捷明了.用导数研究函数的性质比用初等方法研究要方便得多,因此,导数在函数中的应用作为高考命题重点应引起高度注意.考查的方向还是利用导数求函数的极大(小)值,求函数在连续区间[a,b]上的最大值或最小值,或利用求导法解应用题.研究函数的单调性或求单调区间等,这些已成为高考的一个新的热点问题.利用导数的几何意义作为解题工具,有可能出现在解析几何综合试题中,复习时要注意到这一点.
复习措施:
(1)紧扣教材,准确把握概念、法则,夯实学生解题的规范性。
(2)抓主线,攻重点,针对重点内容,结合前几年高考题,重点知识点重点突破。
(3)重视转化、数形结合和分类讨论思想方法的运用
(4)注意本部分知识与其它章节的联系,对与知识的交汇问题,重点放在逻辑思维、推理能力的培养上,尽量减少繁杂运算。要充分利用建模思想。
2.本单元在高考中的地位和作用
导数是研究函数的有力工具,是对学生进行理性思维训练的良好素材。导数在处理单调性、最值等问题时,能降低思维难度,简化解题过程. 其地位由解决问题的辅助工具上升为解决问题的有力工具,因此导数的应用是导数的重点内容,
从近几年的高考命题分析,对导数主要考查导数的几何意义、导数的基本性质和应用以及综合推理能力,这三个热点.可分为三个层次:
第一层次是主要考查导数的概念和某些实际背景(如瞬时速度、加速度、切线的斜率等),求导公式(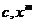 (
(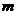 为有理数),
为有理数),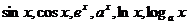 的导数)和求导法则
的导数)和求导法则
第二层次是导数的应用,包括求函数的极值,求函数的单调区间,证明函数的单调性等;
第三层次是综合考查,包括解决应用问题,将导数内容和传统内容中有关不等式和函数的单调性、函数的零点、解析几何中的切线问题等有机的结合在一起,设计综合试题。
在高考中导数的应用主要有以下四方面:①导数的几何意义;②可导函数的单调性与其导数的关系;③可导函数的极值与其导数的关系;④可导函数的最值与其导数的关系.
另外导数的思想方法和基本理论有着广泛的应用,除对中学数学有重要的指导作用外,也能在中学数学的许多问题上起到居高临下和以繁化简的作用。如函数单调性、最值等函数问题;在掌握导数的相关概念的基础上;应用导数作出特殊函数的图象;应用导数解题的一般方法证明某些不等式的成立和解决数列的有关问题,再根据导数所具有的几何意义对切线相关问题及平行问题等几何问题进行了一些探讨,并最终运用导数解决实际问题的最值。 因此导数的应用为高考考查函数提供了广阔天地,处于一种特殊的地位,是高中数学知识的一个重要交汇点,是联系多个章节内容以及解决相关问题的重要工具。
1.本单元近几年来高考试题统计分析
近几年高考试题统计分析(以山东为例)
纵向比较近几年山东的高考题:
理科07年考察了函数的单调性,求函数的极值点,证明不等式。
08年求函数的极值,证明不等式。
09年解应用题求最值。
文科 07年考察了函数的极值点及求函数的极值。
08年考察了知函数的极值点求参数,判断函数的单调性,比较代数式的大小
09年求函数的极值,求参数的取值范围。
横向比较2009年各省的考试题
有以下几点体会.
(1)所涉及的题目类型:主要有6类
①应用题:山东理,湖南理。
②求参数的取值范围:山东文,海南宁夏文,天津文,浙江文理,福建文,全国卷Ⅱ文理,北京理,重庆文,四川理,陕西文理。
③判断函数的单调性或求单调区间:海南宁夏理,江苏,广东文,天津文理,辽宁文,
福建文理,安徽文理,全国卷Ⅰ及Ⅱ的文理,北京文理,重庆文,江西理,四川理,
陕西文理。
④证明不等式:海南宁夏理,辽宁文理。
⑤具体函数的极值,最值及切线方程间的运算:江苏,辽宁文。
⑥创新题:导数和函数,方程,不等式,线性规划及函数的零点的结合题。
如全国卷Ⅰ理,天津卷文。
(2)题目特点及分析:
①与导数有关的题目多为高档题。多和方程,不等式,函数联系。
②原函数多为三次函数、指数函数与二次函数结合或对数函数与二次函数结合,求导后多转化为定义在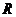 上的二次函数,或定义域为某一区间的二次函数,
上的二次函数,或定义域为某一区间的二次函数,
如:2009年全国(理22(本小题满分12分)
设函数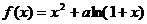 有两个极值点
有两个极值点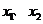 ,且
,且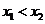
(I)求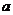 的取值范围,并讨论
的取值范围,并讨论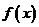 的单调性;(II)证明:
的单调性;(II)证明: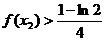
③导数的应用涉及面广,考查的范围大,但与定积分有关的题目基本没有,希望引起同仁的注意,这也是在考试范围之内。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com