
学生自我总结
作业:P23习题1.2A组 1,2,3
练习1.例2变式求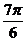 的正弦、余弦和正切值。
的正弦、余弦和正切值。
练习2.问题9:通过观察摩天轮的旋转,三角函数的角的终边所在象限不同,请说说三角函数在各个象限内的三角函数值的符号?独立完成课本P15的“探究”。
[设计意图]:练习1、练习2的设计与例2、例3衔接,主要目的是帮助学生巩固三角函数的本质特征,引导学生从定义出发利用坐标平面内的点的坐标特征自主探究三角函数的有关问题的思想方法。并在特殊情形中体会数形结合的思想方法。
例1.(课本P14例2)已知角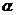 终边经过点
终边经过点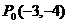 ,求角
,求角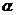 的正弦、余弦和正切值。
的正弦、余弦和正切值。
[分析]:让学生现学现卖,得用上面的定义二就可以得到答案。
例2.(课本P14例1)求 的正弦、余弦和正切值。
的正弦、余弦和正切值。
[学生自主探究]: 让学生自己思考并独立完成。然后与课本的解答相对比一下,发现本题的难点。
让学生自己思考并独立完成。然后与课本的解答相对比一下,发现本题的难点。
[教师讲解]:本题题意很简单,但是如何入手却是难点,关键是对本节课的三角函数定义的要点有没有领会清楚(任意角三角函数的定义要点:点、点的坐标、点到顶点的距离),因此本题的重点之处是如何利用单位圆找到这个点P,如图4可以知道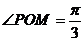 ,又点P在第四象限,得到
,又点P在第四象限,得到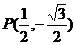 ,这样就可以很容易得到本题答案。
,这样就可以很容易得到本题答案。
不妨让学生取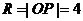 ,能否也得到点P的坐标,得到的三角函数值是否与单位圆的一样。这样可以让学生更深刻体验三角函数的定义。
,能否也得到点P的坐标,得到的三角函数值是否与单位圆的一样。这样可以让学生更深刻体验三角函数的定义。
如图3,已知点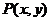 为角
为角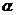 终边上的点,点
终边上的点,点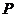 到顶点
到顶点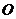 的距离为R,则
的距离为R,则
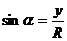 (
(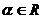 )
)
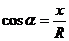 (
(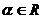 )
)
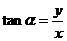 (
(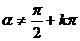 )
)
[分析]:让学生通过刚才的模型进一步体验任意角三角函数的定义要点:点、点的坐标、点到顶点的距离。
问题8:当摩天轮的半径R=1时,三角函数的定义会发生怎样的变化。
[学生自主探究]: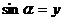 ,
,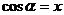 ,
,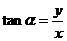 。
。
教师引导学生进行对比,学生通过对比发现取到原点的距离为1的点可以使表达式简化。
教师进一步给出单位圆的定义
给出下列表格,让学生自己补充完整。
|
三角函数 |
定义一: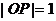 |
定义二: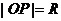 |
定义域 |
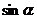 |
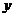 |
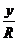 |
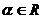 |
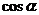 |
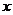 |
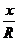 |
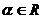 |
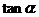 |
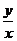 |
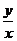 |
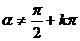 |
及时归纳总结有利学生对所学知识的巩固和掌握。
问题3:请问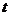 的范围呢?随着时间的推移,你离地面的高度
的范围呢?随着时间的推移,你离地面的高度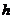 为多少?能不能猜想
为多少?能不能猜想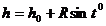 ?
?
[分析]:若想做到这一点,就得把锐角的正弦推广到任意角的正弦。今天我们就要来学习任意角的三函数角函数。
问题4:如图建立直角坐标系,设点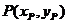 ,能你用直角坐标系中角的终边上的点的坐标来表示锐角
,能你用直角坐标系中角的终边上的点的坐标来表示锐角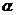 的正弦函数的定义吗?能否也定义其它函数(余弦、正切)?
的正弦函数的定义吗?能否也定义其它函数(余弦、正切)?
[学生自主探究]: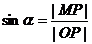
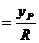
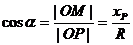 ,
,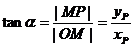
问题5:改变终边上的点的位置,这三个比值会改变吗?为什么?
[分析]:先由学生回答问题,教师再引导学生选几个点,计算比值,获得具体认识,并由相似三角形的性质证明。
[设计意图]:让学生深刻理解体会三角函数值不会随着终边上的点的位置的改变而改变,只与角有关系。
通过摩天轮的演示,让学生感受到第一象限角的正弦可以跟锐角正弦的定义一样。
 问题6:大家根据第一象限角的正弦函数的定义,能否也给出第二象限角的定义呢?
问题6:大家根据第一象限角的正弦函数的定义,能否也给出第二象限角的定义呢?
[学生自主探究]:学生通过上面已知知识得到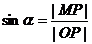
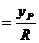
学生定义好第二象限角后,让学生自己算出摩天轮座舱在第150秒时,离地面的高度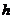 ?
?
通过摩天轮知道: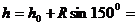
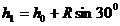
由此得到: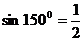
[设计意图]:通过这个,让学生检验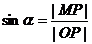
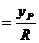 在第二象限角是否正确?
在第二象限角是否正确?
问题7: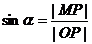 在第三象限角或第四象限能成立吗?
在第三象限角或第四象限能成立吗?
[设计意图]:让学生通过模型,检验定义是否正确,从中让学生自己发现正、负符号的偏差。
(可以让学生取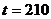 ,从而
,从而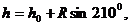 得到
得到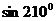 =
=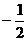 ,发现这与
,发现这与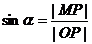 不相符,实际上是
不相符,实际上是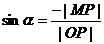 )
)
[教师总结]:我们通过个模型知道如何在某些范围内如何计算自已此时离地面的高度,用数学模型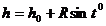 来表示,当摩天轮转动,角度的概念也不知不觉地推广到任意角,对于任意角的正弦不能只是依赖于角所在的直角三角形中的对边的长度比斜边长度了,我更应该用点P的横坐标来代替
来表示,当摩天轮转动,角度的概念也不知不觉地推广到任意角,对于任意角的正弦不能只是依赖于角所在的直角三角形中的对边的长度比斜边长度了,我更应该用点P的横坐标来代替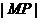 或
或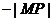 ,那么这样就能够很好表示出正弦的函数任意角的定义。
,那么这样就能够很好表示出正弦的函数任意角的定义。
让学生自主思考如何解决问题:“过了30秒后,你离地面的高度为多少?”
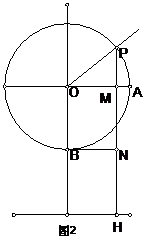 [分析]:作图如图2很容易知道:从起始位置OA运动30秒后到达P点位置,由题意知
[分析]:作图如图2很容易知道:从起始位置OA运动30秒后到达P点位置,由题意知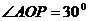 ,作PH垂直地面交OA于M,又知MH=
,作PH垂直地面交OA于M,又知MH=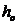 ,所以本问题转变成求PH再次转变为求PM。
,所以本问题转变成求PH再次转变为求PM。
要求PM就是回到初中所学的解直角三角形的问题即锐角的三角函数。
问题2:锐角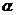 的正弦函数如何定义?
的正弦函数如何定义?
[学生自主探究]:学生很容易得到

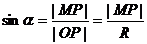
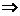
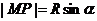
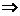
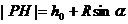
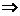
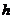
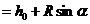
所以学生很自然得到“过了30秒后,过了45秒,你离地面的高度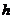 为多少?”
为多少?”
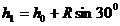
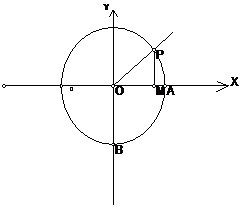
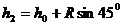
[教师总结]: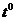 在锐角的范围中,
在锐角的范围中,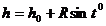
问题1:如图是一个摩天轮,假设它的中心离地面的高度为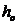 ,它的直径为2R,逆时针方向匀速转动,转动一周需要360秒,若现在你坐在座舱中,从初始位置OA出发(如图1所示),过了30秒后,你离地面的高度
,它的直径为2R,逆时针方向匀速转动,转动一周需要360秒,若现在你坐在座舱中,从初始位置OA出发(如图1所示),过了30秒后,你离地面的高度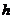 为多少?过了45秒呢?过了
为多少?过了45秒呢?过了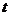 秒呢?
秒呢?
[设计意图]:高中学生已经具有丰富的生活经验和一定的科学知识,因此选择感兴趣的、与其生活实际密切相关的素材,此情景设计应该有助于学生对知识的发生发展的理解。这个数学模型很好融合初中对三角函数的定交,也能放在直角坐标系中,很好地将锐角三角函数的定义向任意角三角函数过渡,揭示函数的本质。
2.教学难点:正弦、余弦、正切函数的定义域.
具体设计如下:
1.教学重点:任意角三角函数的定义.
3.能初步应用定义分析和解决与三角函数值有关的一些简单问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com