新教材的教学理念之一是让学生去体验新知识的发生过程，这节《任意角三角函数》的教案，主要围绕这一点来设计。

到底应该怎样去合理定义任意角的三角函数呢？让学生提出自己的想法，同时让学生去辨证这个想法是否是科学的？因为一个概念是严谨的，科学的，不能随心所欲地编造，必须去论证它的合理性，至少这种概念不能和锐角三角函数的定义有所冲突。在这个立－破的过程中，让学生去体验一个新的数学概念可能是如何形成，在形成的过程中可以从哪些角度加以科学的辩思。这样也有助于学生对任意角三角函数概念的理解。

再次，让学生充分体会在任意角三角函数定义的推广中，是如何将直角三角形这个“形”的问题，转换到直角坐标系下点的坐标这个“数”的过程的。培养数形结合的思想。

上杭县明强中学　 范福太

点评

　“任意角的三角函数的定义”这一节，是三角函数这一章的重要概念。本课从概念的生成发展及建构过程入手，通过几个积极主动的数学活动进行有目的地概念建构和思维训练，以严谨的、科学、理性的思考把“培养学生分析解决问题的能力”贯穿在课堂教学始终。本设计由复习直角三角形中的锐角三角函数开始，到以象限角为载体的锐角三角函数，再到象限角为载体的任意角的三角函数，从中展开问题教学，引导学生从已知到未知、从易到难、由浅入深地进行思维，探究得任意角的三角函数的生成过程。

课程安排自学例题、自做教材练习题，一般性与特殊性相结合，使得学生很好地理解了任意角的三角函数的定义。学生通过教师设计的变式练习，巩固和加深了对三角函数定义的理解。同时此处以问题形式让学生自己归纳识记本节课的主体内容，抓住要害，人人参与，及时建构知识网络，优化知识结构，培养认知能力.这种设计，有效地展示了知识的发生与发展过程，加深了对函数一般概念的理解，体现了学生是学习主体的理念。

不足之处；各教学环节的阶段性目标、重、难点内容的突出、入微的分析、突破难点的重要环节的思考分析不够。

14、函数的图象

1．书面作业：习题1.2第1、2题.

3．你如何记忆正弦、余弦、正切函数值的符号？(根据定义，想象坐标位置， -----)

设计意图：

遗忘的规律是先快后慢，回顾再现是记忆的重要途径，在课堂内及时总结识记主要内容是上策. 此处以问题形式让学生自己归纳识记本节课的主体内容，抓住要害，人人参与，及时建构知识网络，优化知识结构，培养认知能力.

2．你如何判断和记忆正弦、余弦、正切函数的定义域？(根据定义，------)

要求全体学生根据教师所提问题进行总结识记，提问检查并强调：

1．你是怎样把锐角三角函数定义推广到任意角的？或者说任意角三角函数具体是怎样定义的？(建立直角坐标系，使角的顶点与坐标原点重合，---，在终边上任意取定一点P，---)

2、角α的终边经过点P(－3，-4)，求α的正弦，余弦及正切值.　　　　

课堂练习：

p17题1、2、3

处理：要求取点用定义求解，针对计算过程提问、点评，理解巩固定义.

强调：终边在坐标轴上的角叫轴线角，如0、π/2 、π、3π/2 等，今后经常用到轴线角的三角函数值，要结合三角函数定义记熟这些值.

设计意图：

及时安排自学例题、自做教材练习题，一般性与特殊性相结合，进行适量的变式练习，以巩固和加深对三角函数概念的理解，通过课堂积极主动的练习活动进行思维训练，把“培养学生分析解决问题的能力”贯穿在每一节课的课堂教学始终.

1、自学 例1：求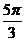的正弦、余弦和正切值。

(情景5)能判断三角函数值的正、负吗？试试看！

引导学生紧紧抓住三角函数定义来分析，r＞0,三角函数值的符号决定于x、y值的正负，根据终边所在位置总结出形象的识记口诀：

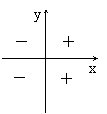
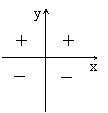
sinα= y/r：上正下负横为0　　 cosα=x/r：左负右正纵为0　

　tanα=y/x：交叉正负

设计意图：

判断三角函数值的正负符号，是本章教材的一项重要的知识、技能要求. 要引导学生抓住定义、数形结合判断和记忆三角函数值的正负符号，并总结出形象的识记口诀，这也是理解和记忆的关键.

2、布置任务情景：什么是三角函数的定义域？请求出三个三角函数的定义域，填写下表：

引导学生自主探索：

如果没有特别说明，那么使解析式有意义的自变量的取值范围叫做函数的定义域，三角函数的定义域自然是指：使比值有意义的角α的取值范围.

关于sinα=y/r、cosα=x/r，对于任意角α(弧度数)，r＞0，y/r、x/r恒有意义，定义域都是实数集R.

对于tanα=y/x，α= kπ+π/2 时x=0，y/x无意义，tanα的定义域是：{α|α∈R，且α≠kπ+π/2 }.　 … … …

教师指出: sinα、cosα、tanα的定义域必须紧扣三角函数定义在理解的基础上记熟。

设计意图：

定义域是函数三要素之一，研究函数必须明确定义域. 指导学生根据定义自主探索确定三角函数定义域，有利于在理解的基础上记住它、应用它，也增进对三角函数概念的掌握.