2、拓展与提高：

已知与都是非零向量，且+3 与7 -5垂直，-4与 7-2垂直，求与的夹角。(本题供学有余力的同学选做)

［设计意图］：通过设计不同层次的作业既使学生掌握基础知识，又使学有余力的学生有所提高，从而达到激发兴趣和“减负”的目的。

1、课本P₁₁₉习题2.4A组1、2、3。

4、类比向量的线性运算，我们还应该怎样研究数量积？

［设计意图］：通过学生讨论总结，加强了学生概念法则的理解和掌握，体会整个内容的研究过程，明白了为什么要学这些内容，学了这些内容可以做什么，这对以后的学习有什么指导意义。

活动七：布置作业

3、我们是按照怎样的思维模式进行概念的归纳和性质的探究？在运算律的探究过程中，渗透了哪些数学思想？

2、平面向量的数量积有哪些应用？

1、本节课我们学习的主要内容是什么？

5、反馈练习

(1)判断下列各题正确与否：

①、若≠0，则对任一非零向量，有·≠0．

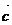②、若≠0，·＝·，则＝．

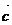(2)　　 已知△ABC中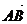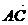，=, =，当· <0或·＝0时，试判断△ABC的形状。

［设计意图］：1.加强学生的练习。2.通过观察、问答等方式对学生的掌握情况有了进一步的了解和把握。

活动六：小结

4、师生共同完成：已知︱︱=3，︱︱=4, 且 与不共线，k为何值时，向量+k与-k互相垂直？并讨论：通过本题，你有什么体会？

［设计意图］：学会利用数量积来解决垂直问题，体会用数量积将几何问题转化为方程求解，体现向量的工具性。

3、学生独立完成：对任意向量 ，b是否有以下结论：

(1)(+)²=²+2·+²　　　　

(2)(+ )·(-)= ²-²

［设计意图］：让学生体会解题中运算律的作用，比较向量运算与数运算的异同。

2、师生共同完成：已知︱︱=6，︱︱=4, 与的夹角为60°，求(+2 )·(-3)，并思考此运算过程类似于哪种实数运算？