
2、规定:零向量与任何向量的数量积为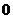 。
。
1、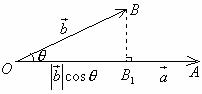 仿照物理问题建构“数学模型”。引入“向量数量积”的概念:已知两个非零向量
仿照物理问题建构“数学模型”。引入“向量数量积”的概念:已知两个非零向量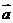 与
与 ,把数量
,把数量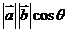 叫做
叫做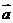 与
与 的数量积(或内积),记作:
的数量积(或内积),记作: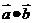 ,即
,即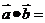
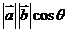 (其中
(其中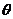 是
是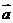 与
与 的夹角)。
的夹角)。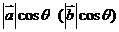 叫做向量
叫做向量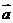 在
在 方向上(
方向上( 在
在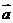 方向上)的投影。
方向上)的投影。
2、如何确定两个非零向量的数量积的符号,什么情况下值为零?
[设计意图]
使学生从感性到理性去认知数量积的定义。通过对概念的认识、分析和探究,使学生加深理解,并掌握相关的性质及几何意义。同时加深对投影的认识。
[师生互动]
 [情景1]
[情景1]
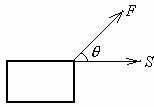
问题 回忆物理中“功”的计算,它的大小与哪些量有关?
结合向量的学习你有什么想法?若一个物体在力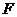 的作用下产
的作用下产
生的位移为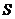 ,那么力
,那么力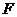 所做的功
所做的功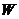 等于多少?
等于多少?
[设计意图]
以物理问题为背景,初步认识向量的数量积,为引入向量的数量积的概念做铺垫。
[师生互动]
生: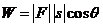 (其中
(其中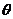 是
是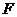 和
和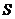 的夹角)。
的夹角)。
师:功是一个矢量还是标量?它的大小由那些量来确定?
显然功是一个标量,它由力和位移两个向量来确定。从中我们得到一个启发:能否将功看成是两个“向量相乘”的一种运算的结果呢?从而得出平面向量的“数量积”的概念。
[情景2]
1、定义向量数量积。弄清定义中涉及哪些量?它们有怎样的关系?运算结果是向量还是数量?
重点是平面向量的数量积的概念和性质;用平面向量数量积表示向量的模及向量的夹角;平面向量数量积的运算律的探究及应用。
难点是平面向量的数量积的定义及对运算律的探究、理解;平面向量数量积的灵活应用。
通过师生互动、学生的自主探究,(1)理解平面向量数量积的含义及其物理意义;(2)掌握向量数量积的性质和运算律,会进行平面向量数量积的运算;(3)能运用数量积表示两个向量的夹角,会用数量积判断两个向量的垂直关系;(4)通过向量的线性运算及多项式乘法运算的对照,强化学生的类比思想;通过数量积的性质、运算律的灵活应用,发展学生从特殊到一般的能力,培养学生学习的主动性和合作交流的学习习惯。
《高中数学课程标准》指出:“有效的数学学习活动不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习数学的重要方式”,转变学生的学习方式,激发学生的学习积极性,让学生乐于参与到探索性和创造性的学习活动中来,这是新课程数学教学的基本要求。《高中数学课程标准》还明确提出了提高学生的知识与技能、重视学生的学习过程与方法,培养学生的情感态度、价值观的三维目标。为此,结合本节课的教学内容,教学中注重过程、方法,注重引导学生自觉去看书,不断提出问题,研究问题,并解决问题。重视在师生,生生互动、交流的过程中渗透情感态度与价值观。
本节以力对物体做功作为背景,研究平面向量的数量积。但是,学生作为初学者不清楚向量数量积是数量还是向量,寻找两向量的夹角又容易想当然,以及对运算律的理解和平面向量的数量积的灵活应用。通过情景创设、探究和思考引导学生认知、理解并掌握相关的内容。利用向量数量积运算讨论一些几何元素的位置关系、距离和角,这些刻画几何元素(点、线、面)之间度量关系的基本量学生容易混淆。利用数量积运算来反映向量的长度和两个向量间夹角的关系解决问题,是学生学习本节内容的重点又是难点。由向量的线性运算迁移、引申到向量的乘法运算这是个很自然的过渡,深入浅出、符合学生的认知规律,也有利于明确本节课的教学任务,激发学生的学习兴趣和求知欲望。
以物体受力做功为背景引入数量积的概念,使向量数量积运算与物理知识联系起来;向量数量积与向量的长度及夹角的关系;进一步探究两个向量的夹角对数量积符号的影响及有关的性质、几何意义和运算律。
本节内容安排在《普通高中课程标准实验教科书·数学必修4》(A版)第二章、第4节第1课时。它是平面向量的核心内容,向量的平行、垂直关系是向量间最基本、最重要的位置关系,而向量的夹角、距离又是向量的重要数量特征,向量的数量积恰好是解决问题的一个重要工具。
本节的知识结构:
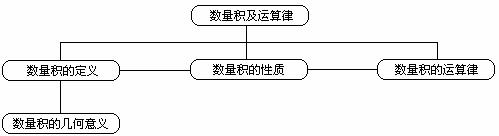
泉州市泉港五中 林文财
点评:
本节课是概念数学课,教师设计了从物理和数学两个角度创设情景,注重概念产生背景及概念深化的过程,使学生认识了数量积的数学模形。通过问题形式引导学生自主探究数量积的性质及运算律,培养了学生类比、从特殊到一般的归纳概括能力,通过练习使学生掌握了数量积的计算,最后教师通过知识技能、思维方法两个方面加以总结,使学生深化对数量积的认识,形成了良好的认知结构。
数量积的性质在解题中有许多应用,同时也应是本节课的重、难点,如何突破,教师在教学设计中似乎“单薄”些。如重要性质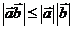 应配备练习来加以巩固。
应配备练习来加以巩固。
17、平面向量数量积的物理背景及其含义(2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com