
4.若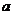 、
、 ∈R+,则
∈R+,则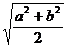 ≥
≥ ≥
≥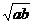 ≥
≥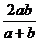 ;当且仅当
;当且仅当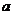 =
= 时等号成立;
时等号成立;
其中包含常用不等式: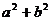 ≥
≥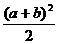 ;
; ≥4以及基本不等式:
≥4以及基本不等式:
 ≥
≥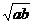 ,基本不等式还有另外两种形式:若
,基本不等式还有另外两种形式:若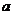 ≤0、
≤0、 ≤0,则
≤0,则 ≤
≤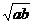 ;
;
若: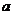 、
、 ∈R,则
∈R,则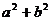 ≥2
≥2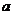
 ;用基本不等式求最值时要关注变量的符号、放缩后是否为定值、等号能否成立(即:一正、二定、三相等,积定和小、和定积大)。
;用基本不等式求最值时要关注变量的符号、放缩后是否为定值、等号能否成立(即:一正、二定、三相等,积定和小、和定积大)。
[举例1] 若直线ax+2by-2=0(a,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则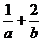 的最小值为 。
的最小值为 。
解析:圆心(2,1),“直线始终平分圆”即圆心在直线上,∴a+b=1,
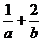 =
=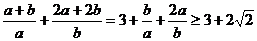 ,当且仅当a=b=
,当且仅当a=b=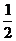 时等号成立。
时等号成立。
[举例2]正数a,b满足a+3=b(a-1),则ab的最小值是 ,a+b的最大值是 。
解析:ab=a+b+3≥2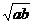 +3
+3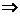
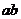 -2
-2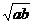 -3≥0
-3≥0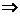
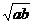 ≥3
≥3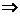
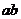 ≥9,当且仅当a=b=3时等号成立。a+b=ab-3≤
≥9,当且仅当a=b=3时等号成立。a+b=ab-3≤ -3
-3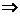
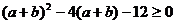
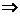 a+b≥6, 当且仅当a=b=3时等号成立。
a+b≥6, 当且仅当a=b=3时等号成立。
注:该方法的实质是利用基本不等式将等式转化为不等式后,解不等式;而不是直接用基本不等式放缩得到最值,因此不存在放缩后是否为定值的问题。
[巩固1]在等式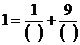 中填上两个自然数,使它们的和最小。
中填上两个自然数,使它们的和最小。
[巩固2]某工厂第一年年产量为A,第二年的年增长率为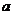 ,第三年的年增长率为
,第三年的年增长率为 ,这两年的平均增长率为
,这两年的平均增长率为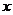 ,则 ( )
,则 ( )
A. B.
B. C.
C. D.
D.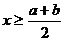
[迁移]甲、乙两人同时从寝室到教室,甲一半路程步行、一半路程跑步,乙一半时间步行、一半时间跑步,如果两人步行速度、跑步速度均相同,则:
A.甲先到教室 B.乙先到教室 C.两人同时到教室 D.不能确定谁先到教室
3.关注不等式||x|-|y||≤|x±y|≤|x|+|y|及其等号成立的条件;具体的:xy≥0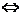
|x+y|=|x|+|y|;xy≥0且|x|≥|y|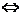 |x-y|=|x|-|y|;xy≥0且|x|≤|y|
|x-y|=|x|-|y|;xy≥0且|x|≤|y|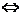 |x-y|=|y|-|x|;
|x-y|=|y|-|x|;
xy≤0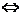 |x-y|=|x|+|y|;xy≤0且|x|≥|y|
|x-y|=|x|+|y|;xy≤0且|x|≥|y|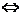 |x+y|=|x|-|y|;xy≤0且|x|≤|y|
|x+y|=|x|-|y|;xy≤0且|x|≤|y|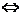
|x+y|=|y|-|x|。
[举例1]若m>0,则|x-a|<m和|y-a|<m是|x-y|<2m的
A.充分而不必要条件, B.必要而不充分条件
C.充要条件 D.既不是充分条件也不是必要条件。
解析:|x-a|<m且|y-a|<m,则|x-y|=|x-a+a-y|≤|x-a|+|y-a|<2m;而当m=4,x=9,y=2,a=2时,
|x-y|=7<2m,但|x-a|=7>m,∴|x-a|<m和|y-a|<m是|x-y|<2m的充分而不必要条件,选A。
[举例2]不等式|2x-log2x|<2x+|log2x|的解集为 。
解析:x>0,不等式|2x-log2x|<2x+|log2x|等价于:|2x-log2x|<|2x|+|log2x|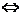 2xlog2x>0
2xlog2x>0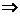
log2x>0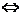 x>1 ∴不等式的解集为(1,+
x>1 ∴不等式的解集为(1,+ )。
)。
[巩固1]a,b都是非零实数,下列四个条件:①|a+b|<|a|+|b|;②|a+b|<|a|-|b|;
③||a|-|b||<|a+b|; ④||a|-|b||<|a-b|;则与|a-b|=|a|+|b|等价的条件是: (填条件序号)。
[巩固2]方程| |=|
|=|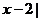 +|
+|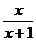 |的解集是 。
|的解集是 。
2.同向不等式相加及不等式的“传递性”一般只用于证明不等式,用它们求变量范围时要求两个不等式中的等号能同时成立。同向不等式一般不能相乘,需增加“两不等式的两边均为正数”才可相乘。
[举例]已知函数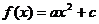 ,且满足-2≤f(1)≤-1,2≤f(2)≤3,则f(3)的取值范围是:
,且满足-2≤f(1)≤-1,2≤f(2)≤3,则f(3)的取值范围是:
。
解析:解决本题的一个经典错误如下:-2≤a+c≤-1 ①; 2≤4a+c≤3 ②
由①得: 1≤-a-c≤2 ③ 4≤-4a-4c≤8 ④
由③+②得:1≤a≤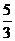 ⑤ 由④+②得:
⑤ 由④+②得:
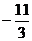 ≤c≤-2 ⑥
≤c≤-2 ⑥
由⑤×9+⑥得: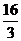 ≤9a+c≤13 ⑦,即
≤9a+c≤13 ⑦,即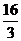 ≤f(3)≤13。错误的原因在于:
≤f(3)≤13。错误的原因在于:
当且仅当1=-a-c且2=4a+c时⑤式中的1=a成立,此时,a=1,c=-2;
当且仅当-4a-4c=8 且4a+c=3 时⑥式中的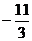 =c成立,此时,a=
=c成立,此时,a=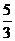 ,c=
,c=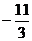 ;
;
可见⑤⑥两式不可能同时成立,所以⑦中的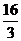 =9a+c不成立;同理,9a+c=13也不成立。
=9a+c不成立;同理,9a+c=13也不成立。
正解是待定系数得f(3)=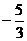 f(1)+
f(1)+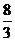 f(2),又:
f(2),又: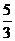 ≤
≤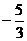 f(1)≤
f(1)≤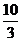 ;
;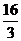 ≤
≤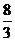 f(2)≤8
f(2)≤8
∴7≤f(3)≤ 。在此过程中虽然也用了“同向不等式相加”,但由错解分析知:当a=1,
。在此过程中虽然也用了“同向不等式相加”,但由错解分析知:当a=1,
c=-2时,不等式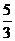 ≤
≤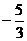 f(1)和
f(1)和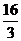 ≤
≤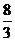 f(2)中的等号同时成立,即f(3)=7成立;而当a=
f(2)中的等号同时成立,即f(3)=7成立;而当a=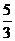 ,c=
,c=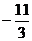 时,不等式
时,不等式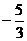 f(1)≤
f(1)≤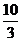 和
和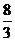 f(2)≤8中的等号同时成立,即f(3)=
f(2)≤8中的等号同时成立,即f(3)= 成立;所以这个解法是没有问题的。可见,在求变量范围时也并非绝对不能用“同向不等式相加”,只要“等号”能同时成立即可;对不含等号的同向不等式相加时则需它们能同时“接近”。
成立;所以这个解法是没有问题的。可见,在求变量范围时也并非绝对不能用“同向不等式相加”,只要“等号”能同时成立即可;对不含等号的同向不等式相加时则需它们能同时“接近”。
注:本题还可以用“线性规划”求解:在约束条件-2≤f(1)≤-1,2≤f(2)≤3下求目标函数f(3)的最大、最小值。
[巩固]设正实数a、b、c、x、y,且a、b、c为常数,x、y为变量,若x+y=c,则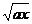 +
+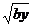 的最大值是:
的最大值是:
A. B.
B. C.
C.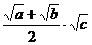 D.
D.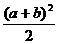
1.在不等式两边非负的条件下能同时平方或开方,具体的:当a>0,b>0时,a>b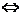 an>bn;
an>bn;
当a<0,b<0时,a>b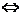 a2<b2;a2>b2
a2<b2;a2>b2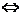 |a|>|b|。在不等式两边同号的条件下能同时取倒数,但不等号的方向要改变,如:由
|a|>|b|。在不等式两边同号的条件下能同时取倒数,但不等号的方向要改变,如:由 <2推得的应该是:x>
<2推得的应该是:x>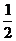 或x<0,而由
或x<0,而由 >2推得的应该是:
>2推得的应该是:
0<x<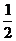 (别漏了“0<x”)等。
(别漏了“0<x”)等。
[举例]若 =
=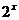 ,则
,则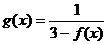 的值域为
;
的值域为
;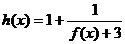 的值域为
。
的值域为
。
解析:此题可以“逆求”:分别用g(x)、h(x)表示f(x),解不等式f(x)>0即可。以下用“取倒数”求:3-f(x)<3,分两段取倒数即0<3-f(x)<3得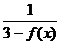 >
>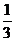 或3-f(x)<0得
或3-f(x)<0得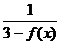 <0,
<0,
∴g(x)∈(- ,0)∪(
,0)∪(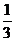 ,+
,+ );f(x)+3>3
);f(x)+3>3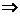 0<
0<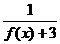 <
<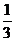
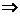 1<h(x)<
1<h(x)<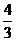 。
。
[巩固1] 若 ,则下列不等式①
,则下列不等式① ;②
;②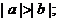 ③
③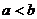 ;④
;④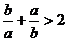 中,正确的不等式有 ( )
中,正确的不等式有 ( )
A.1个 B.2个 C.3个 D.4个
[巩固2] 下列命题:①若a>b,则ac2>bc2;②若ac2>bc2,则a>b;③若a>b,c>d则a-d>b-c;
④若a>b,则a3>b3;⑤若a>b,则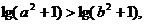 ⑥若a<b<0,则a2>ab>b2;
⑥若a<b<0,则a2>ab>b2;
⑦若a<b<0,则|a|>|b|;⑧若a<b<0,则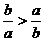 ;⑨若a>b且
;⑨若a>b且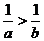 ,则a>0,b<0;
,则a>0,b<0;
⑩若c>a>b>0,则 ;其中正确的命题是 。
;其中正确的命题是 。
[迁移]若a>b>c且a+b+c=0,则:①a2>ab,②b2>bc,③bc<c2,④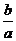 的取值范围是:(-
的取值范围是:(-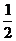 ,1),
,1),
⑤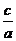 的取值范围是:(-2,-
的取值范围是:(-2,-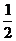 )。上述结论中正确的是
。
)。上述结论中正确的是
。
4、来源于生活实际,又回到生活中,强调了数学应用意识。
福建省周宁第一中学 张徐生
点评:
本课通过精心设计“发现和解决问题”的过程,注重讲背景、讲过程、讲应用,引导学生主动学习、勇于探索。首先从具体问题情境出发,在教师的指导下,结合学生的已有知识经验,通过自主学习,进行发散式猜想与探究判断,去伪存真,提炼猜想,并通过实验验证,完善猜想。其次,在定理证明阶段,通过新旧知识的连接点设问,搭建知识脚手架,让学生展开联想,力求引导学生寻找合理的知识方法(如本课知识生长点:三角函数与平面向量两大工具),进行自主性的活动与尝试,进一步拓展学生知识链。
整节课的设计体现从特殊到一般再回到特殊的研究方法。定理教学体现了教师指导下的学生再创造,充分发挥了学生学习的主动性,让学生在自主探究、实验、猜测、推理中感受和体验,较好地培养与提高了学生发现问题与解决问题、类比与猜想、联想与引申等能力以及探索精神与创新意识。此外,本节课的设计还关注多媒体辅助教学的适当运用,在定理的探求中充分使用了几何画板给予直观演示,强调培养学生应用数学的意识和动手实践的能力;引导学生注意学自己身边的数学,感知生活中包涵的数学现象与数学原理。
3、突出数学的本质。正弦定理的本质是“定量地描写三角形边角之间的关系”,是“大角对大边,小角对小边”的定量化。但量、算、猜不能代替数学思考与逻辑证明,而定理的证明实质是:用垂直做媒介,将一般三角形化为直角三角形处理。本课设计既讲类比联想,又讲逻辑推理,让学生知其然,知其所以然。
2、“用教材教,而不是教教材”,尽管教材中对本课知识方法的要求并不高,只介绍了通过作高将一般三角形变换为直角三角形,再将三角比变换得到等式的化归方法,但教学不仅是忠实执行课程标准,而且是师生共同开发课程,将教材有机裁剪,并融入个性见解的过程。如在正弦定理的证明探究中,学生完全可能围绕“如何构造直角三角形?”,八方联系,广泛联想,分别应用平面几何四点共圆、向量的数量积运算、向量的坐标运算等知识方法。本课设计充分预设各种课堂生成,尽量满足不同思维层次学生的需求。
1、本课就新课程理念下定理教学课的课堂模式,做了一些探索。以问题解决为中心,通过提出问题,完善问题,解决问题,拓展问题,采用实验探究、自主学习的研究性学习方式,重点放在定理的形成与证明的探究上,努力挖掘定理教学中蕴涵的思维价值,培养学生的思辨能力。改变了定理教学中简陋的处理方式(简单直接呈现、照本宣科证明,大剂量的“复制例题”式的应用练习)。
(六)作业布置:
1、书面作业:P10习题1.1 1、2
2、研究类作业:
1)在钝角三角形中探求证明定理的不同方法。
2)在△ABC中, ,研究k的几何意义
,研究k的几何意义
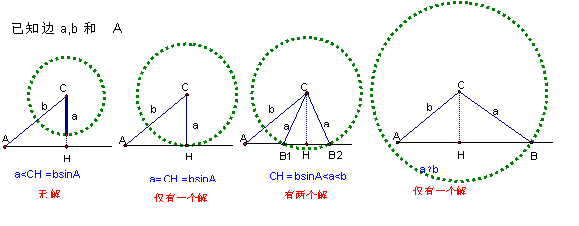
3)已知三角形的两边一角,这个三角形能唯一确定吗?
[设计意图:对问题3),根据分散难点,循序渐进原则,在例2中初步涉及,在课后让学生先行思考,在“正、余弦定理”第三课时中予以下图的剖析阐述。]

(五)课堂小结:
问题5:请同学们用一句话表述学习本课的收获和感受。
生1:原来我只会解直角三角形,现在我会解一般三角形了
师:通过本课学习,你发现自己更强大了。
生2:原来我以为正弦定理的证明,只有书上一种方法,今天我们学到了课本以外的众多方法。
师:我们学习过两个重要数学工具,即三角函数与平面向量,正弦定理的证明充分展示了它们的妙用。
生3:公式很美。
师:美在哪里?
生3:体现了公式的对称美,和谐美······
在同学们的热烈讨论的基础上,用课件展示小结:
1、在正弦定理的发现及其证明中,蕴涵了丰富的思想方法,既有由特殊到一般的归纳思想,又有严格的演绎推理。在定理证明中我们从直观几何角度、向量运算角度探求了数学工具的多样性。
2、正弦定理反映了边与其对角正弦成正比的规律,据此,可以用角的正弦替代对边,具有美学价值
3、利用正弦定理解决三类三角形问题:
(1)已知两角和任一边,求其他两边和一角。
(2)已知两边和其中一边的对角,求另一边 的对角,进而求出其他的边和角。
(3)实现边与角的正弦的互化。
[设计意图:通常,课堂小结均由老师和盘托出,学生接受现成的结论。本设计充分发挥学生思维参与的主动性和创造性,师生合作,让课堂小结成为点睛之笔。]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com