
6. 遇到含参不等式恒成立求参变量的范围问题,通常采用分离参数法,转化为求某函数的最大值(或最小值);具体地:g(a)>f(x)在x∈A上恒成立 g(a)>f(x)max,g(a)<f(x)在x∈A上恒成立
g(a)>f(x)max,g(a)<f(x)在x∈A上恒成立 g(a)<f(x)min,(x∈A)。当参变量难以分离时,也可以用:f(a,x)>0在x∈A上恒成立
g(a)<f(x)min,(x∈A)。当参变量难以分离时,也可以用:f(a,x)>0在x∈A上恒成立 f(a,x)min>0, (x∈A)及f(a,x)<0在x∈A上恒成立
f(a,x)min>0, (x∈A)及f(a,x)<0在x∈A上恒成立 f(a,x)max>0, (x∈A)来转化;还可以借助于函数图象解决问题。特别关注:“不等式f(a,x)≥0对所有x∈M恒成立”与 “不等式f(a,x)≥0对所有a∈M恒成立”是两个不同的问题,前者是关于x的不等式,而后者则应视为是关于a的不等式。特别提醒:“判别式”只能用于“二次函数对一切实数恒成立”的问题,其它场合,概不适用。
f(a,x)max>0, (x∈A)来转化;还可以借助于函数图象解决问题。特别关注:“不等式f(a,x)≥0对所有x∈M恒成立”与 “不等式f(a,x)≥0对所有a∈M恒成立”是两个不同的问题,前者是关于x的不等式,而后者则应视为是关于a的不等式。特别提醒:“判别式”只能用于“二次函数对一切实数恒成立”的问题,其它场合,概不适用。
[举例1]定义在R上的函数f(x)为奇函数,且在[0,+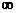
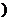 为增函数,对任意
为增函数,对任意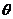 ∈R,不等式f(cos2
∈R,不等式f(cos2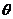 -3)+f(2m-sin
-3)+f(2m-sin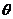 )>0恒成立,则实数m的取值范围是
)>0恒成立,则实数m的取值范围是
解析:∵函数f(x)为奇函数且在[0,+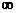
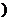 为增函数,易见:函数f(x)为在(-
为增函数,易见:函数f(x)为在(-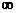 ,0
,0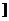 上递增,∴函数f(x) 在(-
上递增,∴函数f(x) 在(-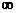 ,+
,+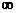
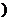 上递增;不等式f(cos2
上递增;不等式f(cos2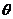 -3)+f(2m-sin
-3)+f(2m-sin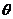 )>0恒成立
)>0恒成立
不等式f(cos2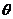 -3)>f(-2m+sin
-3)>f(-2m+sin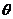 )恒成立
)恒成立 不等式cos2
不等式cos2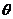 -3>-2m+sin
-3>-2m+sin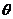 恒成立
恒成立
2m>2sin2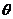 + sin
+ sin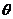 +2恒成立,记g(
+2恒成立,记g(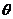 )=2sin2
)=2sin2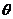 + sin
+ sin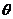 +2=2(sin
+2=2(sin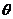 +
+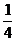 )2+
)2+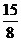 , g(
, g(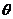 )max=g(1)=5
)max=g(1)=5
∴2m>5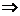 m>
m>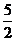 .
.
[举例2]设奇函数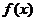 在[-1,1]上是增函数,且
在[-1,1]上是增函数,且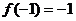 ,若函数
,若函数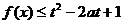 对所有的
对所有的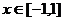 及所有的
及所有的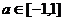 都成立,则
都成立,则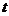 的取值范围是
;
的取值范围是
;
解析:先视x为主元,关于x的不等式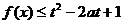 对所有的
对所有的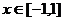 横成立
横成立
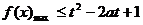 ,又
,又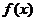 在[-1,1]上递增,∴
在[-1,1]上递增,∴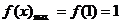 ,即:
,即:
 ≥1,现在视a为主元,关于a的不等式
≥1,现在视a为主元,关于a的不等式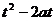 ≥0对所有的
≥0对所有的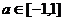 都成立,
都成立,
记g(a)= -2ta+t2,此时分离参数(t)或求函数g(a)的最小值均需讨论,但如果注意到函数g(a)是一次函数,其图象是一条直线,则g(-1) ≥0且g(1) ≥0得t≥2或t≤-2或t=0。
[巩固1]f(x)是偶函数,且f(x)在[0,+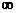
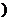 上是增函数,如果f(ax+1)≤f(x-2)在[
上是增函数,如果f(ax+1)≤f(x-2)在[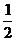 ,1]上恒成立,则实数a的取值范围是
。
,1]上恒成立,则实数a的取值范围是
。
[巩固2]]对满足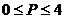 的实数P,做
的实数P,做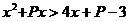 恒成立的x的取值范围是: A.
恒成立的x的取值范围是: A.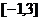 B.
B.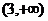 C.
C.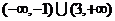 D.
D.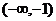
[迁移]已知函数 ,直线
,直线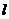 :
: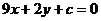 ,若当
,若当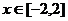 时,函数
时,函数 的图象恒在直线
的图象恒在直线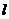 的下方,则
的下方,则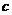 的取值范围是
的取值范围是
简答
5.解决含参变量的无理不等式、含参变量的绝对值不等式、含参变量的指(对数)数不等式问题时常用数形结合。
 [举例1]不等式
[举例1]不等式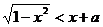 在[-1,1]上恒成立,
在[-1,1]上恒成立,
则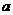 的取值范围是
的取值范围是
解析:分别作函数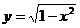 和
和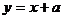 的图象如右,
的图象如右,
前者是以原点为圆心的单位圆的上半部分,后者是斜率
为1的直线。不等式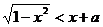 的解即半圆在直线
的解即半圆在直线
的下方的点的横坐标;不等式恒成立即半圆都在直线的下
方,由图可见,只需直线在与圆相切的位置的上方,即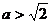 。
。
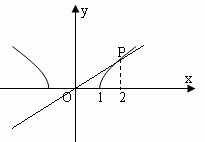
|
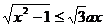 的解集为[1,2],则
的解集为[1,2],则
实数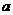 的取值集合是
的取值集合是
解析:分别作函数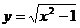 和
和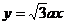 的图象如右,
的图象如右,
前者是双曲线x2-y2=1的x轴上方的部分,后者是过原点
的直线。不等式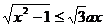 的解即双曲线在直线下方
的解即双曲线在直线下方
的点的横坐标;如图所示,不等式的解集为[1,2],即两图象交点P的横坐标为2,分别代入两函数表达式,得: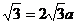 ,即
,即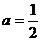 .
.
[巩固1]不等式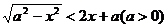 的解集是( )
的解集是( )
A 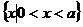 B
B 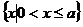 C
C 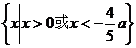 D
D 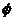
[巩固2]关于x的不等式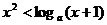 在(0,1)上恒成立,则a的取值范围是 。
在(0,1)上恒成立,则a的取值范围是 。
4.解抽象函数的不等式离不开函数的单调性。抽象函数的不等式反映出的函数值的大小,需借助于函数的单调性化归为自变量的大小,特别注意定义域。画抽象函数的“概念图”是化抽象为形象的有效途径;对某些有具体函数背景的抽象函数,可以从该具体函数中寻找解题线索。
[举例1]已知奇函数f(x)在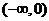 为减函数,f(2)=0则不等式(x-1)f(x-1)<0的解集为:
为减函数,f(2)=0则不等式(x-1)f(x-1)<0的解集为:
 。
。
解析:作函数f(x)的“概念图”如右:
先求不等式xf(x)<0的解:当x>0时
(y轴右侧),f(x)<0(x轴下方),
∴x>2;当x<0时(y轴左侧),
f(x)>0(x轴下方),∴x<-2;可见
不等式xf(x)<0的解为:x<-2或x>2
(也可以根据满足不等式xf(x)<0的函数图象上的点横、纵坐标异号,看图象在第二、四象限的部分得出)。再将x换成x-1,得:x-1<-2或x-1>2即x<-1或x>3。
[举例2]已知函数f(x)对任意实数x、y均有f(x+y)+2=f(x)+f(y),且当x>0时,f(x)>2,f(3)=5,求不等式 f(a2-2a-2)<3的解.
解析:正比例函数f(x)满足:f(x+y)=f(x)+f(y),本题中函数f(x)可视为一次函数。解抽象函数的不等式,需知函数的单调性;用定义:任取x1<x2,x2-x1>0,则f(x2-x1)>2
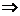 f(x2)+f(-x1)-2>2
f(x2)+f(-x1)-2>2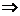 f(x2)+f(-x1)>4;对f(x+y)+2=f(x)+f(y)取x=y=0得:f(0)=2,再取y= -x
f(x2)+f(-x1)>4;对f(x+y)+2=f(x)+f(y)取x=y=0得:f(0)=2,再取y= -x
得f(x)+f(-x)=4即f(-x)=4-f(x),∴有f(x2)+4-f(x1)>4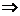 f(x2) > f(x1)
f(x2) > f(x1) 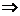 f(x)在R上递增
f(x)在R上递增
又f(3)=f(2)+f(1)-2=f(1)+f(1)-2+f(1)-2=3f(1)-4=5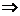 f(1)=3;于是:不等式 f(a2-2a-2)<3
f(1)=3;于是:不等式 f(a2-2a-2)<3
等价于f(a2-2a-2)<f(1) a2-2a-2<1
a2-2a-2<1 -1<a<3。
-1<a<3。
注:(ⅰ)已知抽象函数的运算性质,常用“赋值法”。
(ⅱ)有具体函数背景的抽象函数问题,如果是客观题,可以用具体函数求解。如本题:可设f(x)=kx+b,根据条件求出k、b,再解不等式。
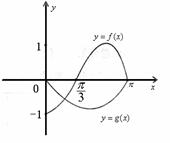 [巩固1]
[巩固1] 是
是
奇函数,它们的定义域均为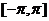 ,且
,且
它们在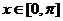 上的图象如图所示,则
上的图象如图所示,则
不等式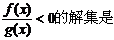
[巩固2]已知定义在正实数集上的函数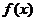 满足①若
满足①若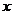 >1,则
>1,则 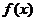 <0;②
<0;②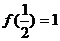 ;③对定义域内的任意实数
;③对定义域内的任意实数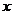 ,
,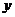 ,都有:
,都有: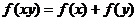 ,则不等式
,则不等式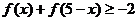
的解集为 。
3.分段函数形成的不等式一般分段解,再取并集;对较为复杂的分段函数问题可以借助于图象解决。
[举例1]设函数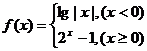 ,若
,若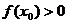 则x0取值范围是 ( )
则x0取值范围是 ( )
A.(-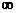 ,-1)∪(1,+
,-1)∪(1,+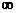 ) B.(-
) B.(-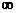 ,-1)∪(0,+
,-1)∪(0,+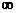 )
)
C.(-1,0)∪(0,1) D.(-1,0)∪(0,+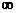 )
)
解析:若x0<0,则f(x0)=lg|x0|>0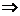 |x0|>1
|x0|>1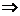 x0<-1;若x0≥0,则f(x0)=
x0<-1;若x0≥0,则f(x0)=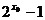 >0
>0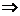 x0>0
x0>0
故选B
[举例2]已知:函数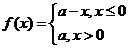 (
(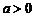 ).解不等式:
).解不等式: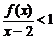 .
.
解析:(ⅰ)当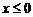 时,即解
时,即解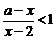
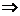
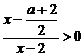 ,此时不等式恒成立,即
,此时不等式恒成立,即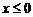 ;
;
(ⅱ)当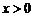 时,即解
时,即解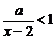
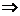
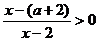 ,∵
,∵ 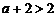 ,
,
∴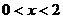 或
或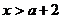 .综上:不等式的解为:
.综上:不等式的解为: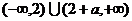
[巩固1]设函数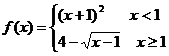 ,则使
,则使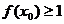 。则x0的取值范围是( )
。则x0的取值范围是( )
A (- ]
]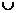 [0,10] B (-
[0,10] B (- ]
]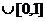 C (
C (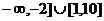 D[-2,0]
D[-2,0]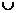 [1,10]
[1,10]
[巩固2]已知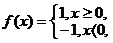 则不等式
则不等式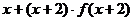 ≤5的解集是
≤5的解集是

2.解绝对值不等式的关键是“去绝对值”,通常有①利用绝对值不等式的性质:若M>0则
|f(x)|>M f(x)>M或f(x)<-M;②平方(不等式两边同正);③讨论(绝对值内的式子为0)。
f(x)>M或f(x)<-M;②平方(不等式两边同正);③讨论(绝对值内的式子为0)。
[举例]设p:x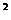 -x-20>0,q:
-x-20>0,q: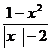 <0,则p是q的 ( )
<0,则p是q的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
解析:p:(-∞,-4) ∪(5,+∞);以下对命题q中的不等式去绝对值:(ⅰ)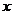 ≥0时
≥0时
原不等式等价于: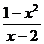 <0
<0
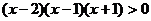
 -1<
-1<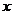 <1或
<1或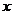 >2;注意到
>2;注意到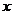 ≥0,
≥0,
∴0≤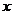 <1或
<1或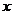 >2;(ⅱ)
>2;(ⅱ)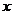 <0时,原不等式等价于:
<0时,原不等式等价于: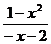 <0
<0
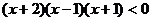
 -1<
-1<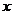 <1或
<1或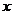 <-2;注意到
<-2;注意到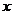 <0, ∴-1<
<0, ∴-1<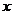 <0或
<0或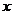 <-2;∴q:(-∞,-2)∪(-1,1)∪(2,+∞)
<-2;∴q:(-∞,-2)∪(-1,1)∪(2,+∞)
可见:p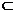 q,故选A。
q,故选A。
[巩固]不等式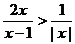 的解集是
.
的解集是
.
[迁移]已知函数 在
在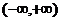 上是增函数,A (0, -2 ), B (4 ,2 )是其图象
上是增函数,A (0, -2 ), B (4 ,2 )是其图象
上的两个点,那么不等式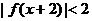 的解集是
的解集是
1.解分式不等式不能轻意去分母,通常采用:移项(化一边为零)→通分→转化为整式不等式→化所有因式中的变量系数为正,(即不等式两边同除以变量系数,若它的符号不能确定即需要讨论)→“序轴标根”(注意比较各个根的大小,不能比较时即需要讨论); [特别关注] 求一个变量的范围时,讨论的也是这个变量,结果要并;讨论的若是另一个变量,结果不能并。
[举例1]关于x的不等式ax-b>0的解集是(1,+∞),则关于x的不等式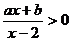 的解集是( )
的解集是( )
A.(-∞,-1)∪(2,+∞) B.(-1,2) C.(1,2) D.(-∞,1)∪(2,+∞)
解析:不等式ax-b>0的解集是(1,+∞)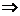 a>0且a=b,则不等式
a>0且a=b,则不等式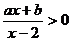 等价于:
等价于:
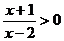
 (x+1)(x-2)>0
(x+1)(x-2)>0 x>2或x<-1,选A。
x>2或x<-1,选A。
[举例2] 解关于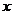 的不等式:
的不等式:
解析:

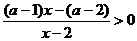

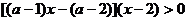
以下不等式两边同除以a-1,需讨论其正负;①若a>1,等价于: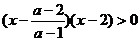
此时需知不等式相应的方程的两根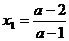 与
与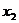 =2的大小,比差:
=2的大小,比差: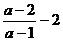 =
=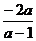 ,
,
可见a>1时,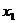 <
<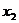 ,∴不等式的解为:(-∞,
,∴不等式的解为:(-∞,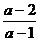 )∪(2,+∞)
)∪(2,+∞)
②若a<1,不等式等价于: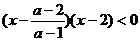 ,(ⅰ)若0<a<1,
,(ⅰ)若0<a<1, 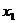 >
>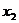 ,不等式的解为:
,不等式的解为:
(2,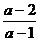 );(ⅱ)若a<0,
);(ⅱ)若a<0,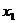 <
<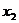 ,不等式的解为:(
,不等式的解为:(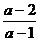 ,2);(ⅲ) 若a=0, 不等式等价于:
,2);(ⅲ) 若a=0, 不等式等价于: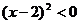 ,不等式的解为
,不等式的解为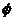 ;综上所述:当a>1时不等式的解为(-∞,
;综上所述:当a>1时不等式的解为(-∞,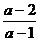 )∪(2,+∞);当0<a<1时不等式的解为(2,
)∪(2,+∞);当0<a<1时不等式的解为(2,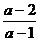 );当a=0时不等式的解为
);当a=0时不等式的解为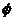 ;当a<0时不等式的解为:(
;当a<0时不等式的解为:(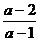 ,2)。
,2)。
[巩固1]若不等式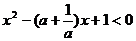 的解为
的解为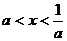 ,则
,则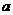 的取值范围是
的取值范围是
[巩固2]解关于x的不等式: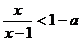
[迁移] 已知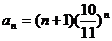 (
(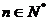 ),则数列
),则数列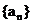 最大项为第 项。
最大项为第 项。
5、[巩固1] 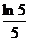 <
<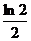 <
<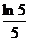 ,[巩固2]A,[迁移]递增;6、[巩固]有理化,[迁移]放缩:
,[巩固2]A,[迁移]递增;6、[巩固]有理化,[迁移]放缩:
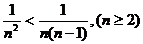 。
。
1.[巩固1]B,[巩固2] ②③④⑥⑦⑨⑩;[迁移] ①③④⑤;2、[巩固]A;3、[巩固1] ①④,
[巩固2](-1,0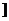 ∪[2, +
∪[2, +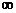 );4、[巩固1]4,12;[巩固2]B,[迁移]B;
);4、[巩固1]4,12;[巩固2]B,[迁移]B;
6.放缩法的方法有:①添加或舍去一些项,如: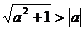 ;
;
②将分子或分母放大(或缩小);③利用基本不等式,如:
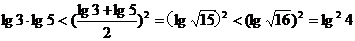 ;
;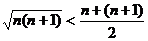 等;
等;
④利用常用结论:下列各式中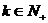
(Ⅰ)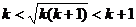 (Ⅱ)
(Ⅱ)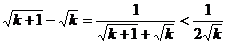 ;
;
(Ⅲ)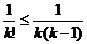
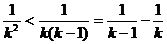
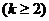 ;
; 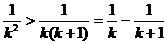 (Ⅳ)
(Ⅳ)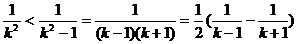
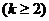 ;
;
[举例]已知a、b、c是⊿ABC的三边长,A=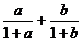 ,B=
,B=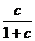 ,则:
,则:
A.A>B, B. A<B, C.A≥B D.A≤B
解析:B=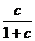 =
=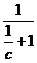 <
<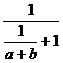 =
=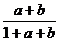 =
=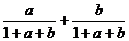 <
<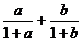 =A
=A
[巩固]若n∈N﹡,求证: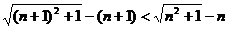
[迁移]已知an=2n-1,数列{an}的前n项和为Sn,bn=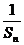 ,数列{ bn}的前n项和为Tn,求证:对一切自然数n,恒有Tn<2。
,数列{ bn}的前n项和为Tn,求证:对一切自然数n,恒有Tn<2。
简答
5.比较大小的方法有:①比差:判断“差”的正负,因式分解往往是关键;②比商:判断“商”与1的大小,两个式子都正才能比商,常用于指数式的比较;③变形:如平方(需为正数)、有理化(根式的和、差)等;④寻求中间变量,常见的有0,1等;⑤数形结合。
用定义证明单调性的过程就是已知自变量的大小比较函数值的大小的过程。
[举例1]已知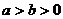 且
且 ,若
,若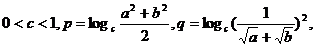 则
则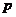 、
、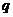 的大小关系是( )
的大小关系是( )
A.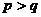 B.
B.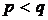 C.
C.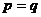 D.
D.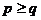
解析:记x=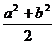 , y=(
, y=(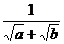 )2, 直接比较x、y的大小将大费周章,但: x>
)2, 直接比较x、y的大小将大费周章,但: x>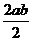 =1,
=1,
y=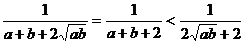 =
=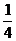 ,∴x>y,又0<c<1,∴
,∴x>y,又0<c<1,∴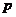 <
<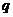 。
。
[举例2] x0是x的方程ax=logax(0<a<1)的解,则x0,1,a这三个数的大小关系是 。
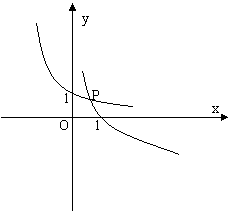 解析:显然方程ax=logax不能用代数方法
解析:显然方程ax=logax不能用代数方法
研究。分别作函数y=ax及y=logax的图象
如右,它们的交点为P(x0,y0),易见
x0<1, y0 <1,而y0=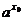 =logax0
=logax0
即logax0<1,又0<a<1,∴x0>a,
即a<x0<1。
[巩固1]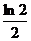 、
、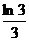 、
、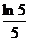 的大小关系是
。
的大小关系是
。
[巩固2]设a>2,p=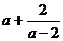 ,q=
,q=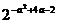 ,则:
,则:
A.p>q B.p<q C.p>q与p=q都有可能 D.p>q与p<q都有可能
[迁移] 设定义在R上的函数f(x)满足:①对任意的实数x,y∈R,有f(x+y)=f(x)·f(y);②当x>0时,f(x)>1;判断并证明函数f(x)的单调性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com