
1.[巩固1]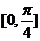 ∪
∪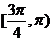 ,[巩固2]A,[迁移]B;2、[巩固]3,[迁移]
,[巩固2]A,[迁移]B;2、[巩固]3,[迁移]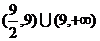 ;3、[巩固]C, [迁移]B;4、[巩固]4x+3y-4=0或x=1;[迁移]将条件变形为:
;3、[巩固]C, [迁移]B;4、[巩固]4x+3y-4=0或x=1;[迁移]将条件变形为:
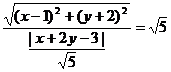 ,由圆锥曲线的统一定义知P点轨迹为双曲线;[提高] 将条件变形为:
,由圆锥曲线的统一定义知P点轨迹为双曲线;[提高] 将条件变形为: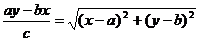 ,问题转化为:直线
,问题转化为:直线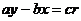 和圆
和圆
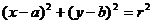 的公共点,于是有:
的公共点,于是有: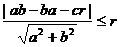 即:c2≤a2+b2;
即:c2≤a2+b2;
7.关注“线性规划”问题的各种“变式”:①“可行域”由不等式和方程共同确定(为线段或射线),②“约束条件”由二次方程的“区间根”间接提供,③“约束条件”非线性,④目标函数非线性,如: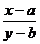 (斜率),
(斜率),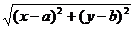 (距离)等。
(距离)等。
 [举例] 实系数方程
[举例] 实系数方程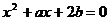 的一个根大于0且小于1,另一个根大于1且小于2,则
的一个根大于0且小于1,另一个根大于1且小于2,则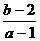 的取值范围是
的取值范围是
解析: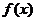 =
=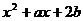 ,数形结合容易得到使实系数方程
,数形结合容易得到使实系数方程
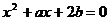 的两根分别在(0,1)和(1,2)内当且仅当:
的两根分别在(0,1)和(1,2)内当且仅当:
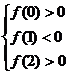
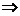
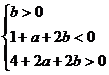 点P(
点P(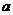 ,
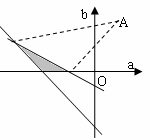
,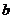 )的可行域如右,
)的可行域如右,
记A(1,2),线段PA的斜率为 ,
, =
=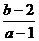 ∈
∈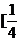 ,1]。
,1]。
[巩固] 若x,y满足:x+y-3≥0,x-y+1=0,3x-y-5≤0,设y=kx,则k的取值范围是________
[提高] 已知不等式ax2+bx+a<0(ab>0)的解集是空集,则a2+b2-2b的取值范围是 。
简答
6.不等式ax+by+c>0(a>0)所表示的区域为直线ax+by+c=0的右侧,不等式ax+by+c<0(a>0)所表示的区域为直线ax+by+c=0的左侧;a﹤0时情况相反。也可以说:不等式ax+by+c>0(b>0)所表示的区域为直线ax+by+c=0的上方,不等式ax+by+c<0(b>0)所表示的区域为直线ax+by+c=0的下方;b﹤0时情况相反。目标函数z=mx+ny(m>0)在“可行域”D内的最值:令mx+ny=0, 在“可行域”D内平移直线mx+ny=0使之位于最左侧,此时z取得最小值; 位于最右侧,此时z取得最大值;m<0时情况相反。如果z=mx+ny(n>0), 也可以说:在“可行域”D内平移直线mx+ny=0使之位于最下方,此时z取得最小值; 位于最上方,此时z取得最大值;n<0时情况相反。若线性目标函数的最优解不止一个,则目标函数为0的直线与“可行域”的一个边界平行或重合。
 [举例] 已知x,y满足约束条件:
[举例] 已知x,y满足约束条件:
2x-y≥0,x+y-2≥0,6x+3y≤18,
且z=ax+y(a>0)取得最小值的最优解
有无穷多个, 求a的值。
解析:要使目标函数取得最小值的最优解
有无穷多个,令ax+y=0并平移使之与过
点C(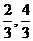 )(可行域中最左侧的点)的边界
)(可行域中最左侧的点)的边界
重合即可,注意到a>0,只能和AC重合,∴a=1
[举例2]已知点P(3,-1)和Q(-1,2),直线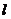 :ax+2y-1=0与线段PQ有公共点,则实数a的取值范围为:
:ax+2y-1=0与线段PQ有公共点,则实数a的取值范围为:
A.1≤a≤3 B.a≤1或a≥3 C.a≤1 D.a≥3
解析:本题可参照“3[举例]⑤⑥”的做法,确定直线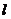 的斜率的范围。现在用不等式所表示的区域解决:直线
的斜率的范围。现在用不等式所表示的区域解决:直线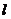 与线段PQ有公共点即点P、Q在直线
与线段PQ有公共点即点P、Q在直线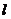 的两侧或在直线
的两侧或在直线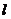 上,记:
上,记:
f (x,y)= ax+2y-1,则f(3,-1)f(-1,2) ≤0,解得:a≤1或a≥3,选B。“3[举例]⑤⑥”也可照此办理。
[巩固1]
已知x,y满足约束条件:2x-y≥0,x+y-2≥0,6x+3y≤18,且z=ax+y取得最大值的最优解恰为(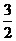 ,3),则a的取值范围是
。
,3),则a的取值范围是
。
[巩固2]点(-2,t)在直线2x-3y+6=0的上方,则t的取值范围是 。
[迁移] 双曲线x2-y2=1右支上一点P(a,b)到直线y=x的距离为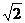 ,则a+b的值是( )
,则a+b的值是( )
A. -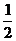 B.
B. 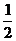 C.
-
C.
-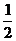 或
或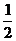 D.2或
D.2或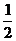
5.点M(m,n)关于直线y=±x+b的对称点M’(±n b,±m+b),即:将M点的坐标代入对称轴方程求得M/的坐标;但对称轴斜率不为±1时,只可根据中、垂建立方程组(即MM/与对称轴垂直且其中点在对称轴上),解出对称点坐标。光线反射问题、角平分线问题、到两定点距离之和(差)的最值问题等都与对称有关。
b,±m+b),即:将M点的坐标代入对称轴方程求得M/的坐标;但对称轴斜率不为±1时,只可根据中、垂建立方程组(即MM/与对称轴垂直且其中点在对称轴上),解出对称点坐标。光线反射问题、角平分线问题、到两定点距离之和(差)的最值问题等都与对称有关。
[举例1]将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合,若此时点C(7,3)与点D(m,n)重合,则m+n的值是 。
解析:“折痕”是AB的中垂线 :y=2x-3,C(7,3)、D(m,n)关于
:y=2x-3,C(7,3)、D(m,n)关于 对称,则:
对称,则:
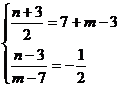
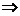
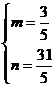
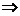 m+n=
m+n=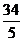 。
。
[举例2]在⊿ABC中,已知A(2,3),角B的平分线为Y轴,角C的平分线为 :x+y=4,求BC边所在的直线方程
:x+y=4,求BC边所在的直线方程
解析:由题意知直线BA、BC关于Y轴对称,即A关于Y轴的对称点A1(-2,3)在直线BC上;直线CA、CB关于 对称,即A关于
对称,即A关于 的对称点A2(1,2)在直线CB上;∴直线BC即直线A1A2:x+3y-7=0,
的对称点A2(1,2)在直线CB上;∴直线BC即直线A1A2:x+3y-7=0,
[巩固]已知点A在x轴上,点B在直线 :y=x上,C(2,1),则⊿ABC的周长的最小值为
。
:y=x上,C(2,1),则⊿ABC的周长的最小值为
。
[迁移] 已知点A(1、1),曲线C上的点(x、y)满足: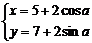 ,一束光线从点A出发经y轴反射到曲线C上的最短路程是:
( )
,一束光线从点A出发经y轴反射到曲线C上的最短路程是:
( )
A 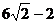 B
B 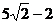 C 8
D 10
C 8
D 10
4.点到直线的距离公式在求三角形的面积、判断直线与圆的位置关系、求圆的弦长、解决与圆锥曲线的第二定义有关的问题等场合均有运用,推导两平行线间的距离公式也是它的一个运用。
[举例] 已知5x+12y=60,则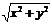 的最小值是:
的最小值是:
A.  B.
B.
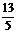 C.
C.
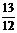 D.
1
D.
1
解析: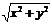 表示直线
表示直线 :5x+12y=60上的动点到原点的距离,其最小值即原点到直线
:5x+12y=60上的动点到原点的距离,其最小值即原点到直线 的距离,选A。注:此题若代入消元、配方求最值则很麻烦。
的距离,选A。注:此题若代入消元、配方求最值则很麻烦。
[巩固]直线 过点(1,0),且被两平行直线3x+y-6=0和 3x+y+3=0所截得的线段长为9,则直线
过点(1,0),且被两平行直线3x+y-6=0和 3x+y+3=0所截得的线段长为9,则直线 的方程为
。
的方程为
。
[迁移] 若动点P(x,y)满足|x+2y-3|=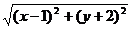 ,则P点的轨迹是:
,则P点的轨迹是:
A.圆 B、椭圆 C、双曲线 D、抛物线
[提高]若a、b、c为实数,恒存在实数x,y,使得ay-bx=c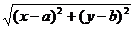 ≠0,则a、b、c满足: A.c2≥a2+b2 B.c2>a2+b2 C.c2<a2+b2 D.c2≤a2+b2
≠0,则a、b、c满足: A.c2≥a2+b2 B.c2>a2+b2 C.c2<a2+b2 D.c2≤a2+b2
3.“到角”的范围:(0,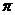 ),“到角公式”就是两角差的正切公式,多用于解决与角平分线有关的问题;“夹角”的范围:(0,
),“到角公式”就是两角差的正切公式,多用于解决与角平分线有关的问题;“夹角”的范围:(0,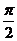
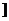 。两直线
。两直线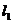 :A1x+B1y+C1=0,
:A1x+B1y+C1=0,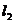 :A2x+B2y+C2=0平行、垂直的条件有“比”和“积”两种形式(重合只有“比式”),如:
:A2x+B2y+C2=0平行、垂直的条件有“比”和“积”两种形式(重合只有“比式”),如: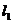 ⊥
⊥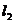
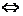 A1A2+B1B2=0,若
A1A2+B1B2=0,若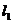 、
、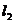 不重合,则
不重合,则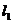 ∥
∥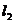
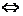 A1B2=A2B1;判断两直线位置关系时要特别注意斜率不存在及斜率为0的情形。
A1B2=A2B1;判断两直线位置关系时要特别注意斜率不存在及斜率为0的情形。
[举例1]直线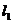 :x=1到直线
:x=1到直线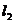 :2x+y+1=0的角是: ( )
:2x+y+1=0的角是: ( )
A.arctan2, B.arctan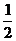 C.
C.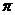 - arctan2 D.
arctan(-
- arctan2 D.
arctan(-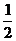 )
)
解析:记直线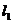 到
到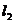 的角为
的角为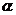 ,直线
,直线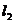 的倾斜角为
的倾斜角为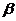 ,作图可见
,作图可见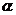 =
=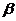 -
-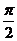 ,tan
,tan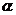 =-cot
=-cot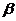
=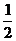 ,故选B。
,故选B。
[举例2]①已知P(x0,y0)是直线 :f(x,y)=0外一点,则直线f(x,y)+f(x0,y0)=0与直线
:f(x,y)=0外一点,则直线f(x,y)+f(x0,y0)=0与直线 的位置关系是 ; ②设a、b、c分别是⊿ABC中角A、B、C的对边,则直线:
的位置关系是 ; ②设a、b、c分别是⊿ABC中角A、B、C的对边,则直线:
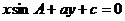 与直线
与直线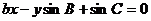 的位置关系是 。
的位置关系是 。
解析:①方程f(x,y)=0与f(x,y)+f(x0,y0)=0两变量的系数完全相同,而f(x0,y0)≠0,即常数项不同,故平行;②由正弦定理知: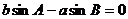 ,故垂直。
,故垂直。
[巩固]已知直线l1的方程为y=x,直线l2的方程为y=ax+b(a,b为实数),当直线l1与l2夹角的范围为[0,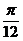
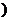 时,a的取值范围是:
时,a的取值范围是:
A.(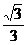 ,1)∪(1,
,1)∪(1,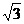 ) ,B.(0,1)
, C.(
) ,B.(0,1)
, C.(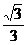 ,
,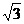 ) , D.(1,
) , D.(1,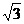 )
)
[迁移]直线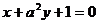 与直线
与直线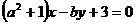 互相垂直,
互相垂直,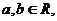 则|
则|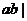 的最小值是:A.1 B.2 C.4 D.5
( )
的最小值是:A.1 B.2 C.4 D.5
( )
2.“点斜式”是直线方程的最基本形式,是其它各种形式的源头,但它不能表示斜率不存在的直线;解决“直线过定点”的问题多用“点斜式”。“斜截式”最能体现直线的函数性质(一次函数,一次项系数是斜率),“斜截式”中所含的参数最少(2个,而其它各种形式中都是3个),所以用待定系数法求直线方程时多设为“斜截式”,它也不能表示斜率不存在的直线。
“截距式”最能反映直线与坐标轴的位置关系;注意:截距是坐标而不是距离;在两坐标轴上截距相等的直线斜率为-1或过原点;“截距式”不能表示斜率为0、斜率不存在以及过原点的直线。“两点式”完全可以由“点斜式”替代,“两点式”不能表示斜率为0和斜率不存在的直线,但它的变形(“积式”):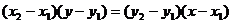 却能表示所有的直线。“一般式”能表示所有的直线,它是直线方程的“终极”形式。
却能表示所有的直线。“一般式”能表示所有的直线,它是直线方程的“终极”形式。
[举例]已知直线 :kx+y-k+2=0和两点A(3,0),B(0,1),下列命题正确的是
:kx+y-k+2=0和两点A(3,0),B(0,1),下列命题正确的是
(填上所有正确命题的序号)。
①直线 对任意实数k恒过点P(1,-2);
对任意实数k恒过点P(1,-2);
②方程kx+y-k+2=0可以表示所有过点P(1,-2)的直线;
③当k=±1及k=2时直线 在坐标轴上的截距相等;
在坐标轴上的截距相等;
④若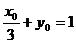 ,则直线
,则直线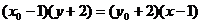 与直线AB及直线
与直线AB及直线 都有公共点;
都有公共点;
⑤使得直线 与线段AB有公共点的k的范围是[-3,1];
与线段AB有公共点的k的范围是[-3,1];
⑥使得直线 与线段AB有公共点的k的范围是
与线段AB有公共点的k的范围是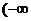 ,-3]∪[1,
,-3]∪[1,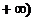 。
。
解析:①直线 :y +2= - k(x
-1)恒过P(1,-2),②方程kx+y-k+2=0不能表示直线x=1,③当k= -1时直线
:y +2= - k(x
-1)恒过P(1,-2),②方程kx+y-k+2=0不能表示直线x=1,③当k= -1时直线 在坐标轴上的截距相反;④若
在坐标轴上的截距相反;④若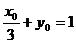 ,则点M(x0,y0)在直线AB上(截距式),又点P(1,-2)在直线
,则点M(x0,y0)在直线AB上(截距式),又点P(1,-2)在直线 ,而直线
,而直线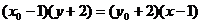 过点M,P(两点式),即与直线AB有公共点M,与直线
过点M,P(两点式),即与直线AB有公共点M,与直线 有公共点P;⑤⑥直线
有公共点P;⑤⑥直线 与线段AB有公共点,不宜先解方程组再解不等式组(麻烦),数形结合易见,直线
与线段AB有公共点,不宜先解方程组再解不等式组(麻烦),数形结合易见,直线 应在直线PA到PB之间,而其间有斜率不存在的位置,故命题⑥正确。
应在直线PA到PB之间,而其间有斜率不存在的位置,故命题⑥正确。
[巩固]已知圆C:x2+(y-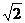 )2=1,则在坐标轴上的截距相等且与圆相切的直线有 条?[迁移] 对任意实数m,直线(m+2)x-(2m-1)y-(3m-4)=0和椭圆
)2=1,则在坐标轴上的截距相等且与圆相切的直线有 条?[迁移] 对任意实数m,直线(m+2)x-(2m-1)y-(3m-4)=0和椭圆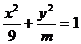 恒有公共点,则m的取值范围是 。
恒有公共点,则m的取值范围是 。
1.直线的倾斜角的范围:[0,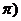 ,x轴及平行于x轴的直线倾斜角是0而不是
,x轴及平行于x轴的直线倾斜角是0而不是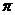 ;y轴及平行于y轴的直线的倾斜角为
;y轴及平行于y轴的直线的倾斜角为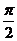 而不是没有倾斜角(只是斜率不存在);已知斜率(的范围)会求倾斜角(的范围),记住:当倾斜角α是锐角时,斜率k与α同增同减,当α是钝角时,k与α也同增同减。斜率的求法:①依据直线方程②依据倾斜角③依据两点的坐标④方向向量(以
而不是没有倾斜角(只是斜率不存在);已知斜率(的范围)会求倾斜角(的范围),记住:当倾斜角α是锐角时,斜率k与α同增同减,当α是钝角时,k与α也同增同减。斜率的求法:①依据直线方程②依据倾斜角③依据两点的坐标④方向向量(以 =(m,n)(m≠0)为方向向量的直线的斜率为
=(m,n)(m≠0)为方向向量的直线的斜率为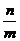 )。关注斜率在求一类分式函数值域时的运用。
)。关注斜率在求一类分式函数值域时的运用。
[举例1]已知两点A(-1,-5),B(3,-2),直线l的倾斜角是直线 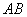 倾斜角的一半,则直线l的斜率为:
.
倾斜角的一半,则直线l的斜率为:
.
解析:记直线l的倾斜角为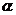 ,则直线AB的倾斜角为2
,则直线AB的倾斜角为2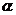 ,其斜率tan2
,其斜率tan2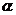 =
=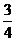
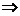
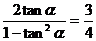
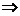 tan
tan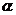 =-3或tan
=-3或tan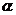 =
=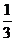 而由tan2
而由tan2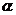 =
=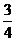 >0得2
>0得2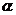 是锐角,则
是锐角,则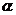 ∈(0,
∈(0,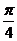 ),
),
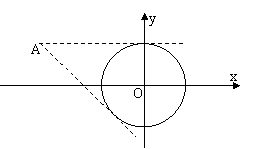 ∴tan
∴tan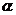 =
=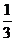 。
。
[举例2] 函数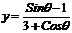 的值域为
。
的值域为
。
解析:记P(cos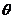 ,sin
,sin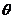 ),A(-3,1)
),A(-3,1)
则y=kPA,P点的轨迹是圆心为原点
的单位圆,如右图:当直线PA与圆相切时,其斜率分别为0和 ,
,
∴y=kPA ∈[ ,0]。注:这里存在一个kPA在0与
,0]。注:这里存在一个kPA在0与 “之间”还是“之外”的问题,原则是其间是否有斜率不存在的情况,若有则在“之外”,若无则在“之间”。
“之间”还是“之外”的问题,原则是其间是否有斜率不存在的情况,若有则在“之外”,若无则在“之间”。
[巩固1] 已知直线 :
: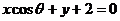 则
则 倾斜角的范围是:
。
倾斜角的范围是:
。
[巩固2]实数x,y满足 的取值范围为 ( )
的取值范围为 ( )
A.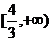 B.
B.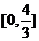 C.
C.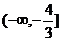 D.
D.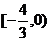
[迁移] 点P是曲线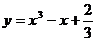 上的动点,设点P处切线的倾斜角为
上的动点,设点P处切线的倾斜角为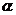 ,则
,则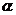 的取值范围是A、
的取值范围是A、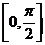 B、
B、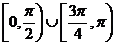 C、
C、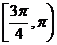 D、
D、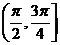
5、[巩固1] 设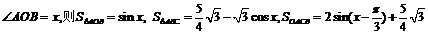 ,
,
当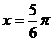 时,
时,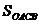 有最大值
有最大值 .[巩固2] 北偏东600,10;
.[巩固2] 北偏东600,10;
3.[巩固1] (0,
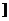 (0,
(0,
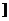 ;[巩固2]450;[迁移]先求A=
;[巩固2]450;[迁移]先求A= ,再用正弦定理求出:b+c=
,再用正弦定理求出:b+c=
6sin(B+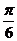 )∈
)∈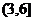 ,于是a+b+c∈(6,9
,于是a+b+c∈(6,9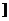 ,也可以用余弦定理;4、[巩固] (1)450,(2)
,也可以用余弦定理;4、[巩固] (1)450,(2)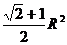 ;[迁移]3或5;
;[迁移]3或5;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com