
4、我们知道,数的加法满足交换律和结合律,即对任意实数a,b,有a+b=b+a
(a+b)+c=a+(b+c)那么对于任意向量 ,
, 向量加法的交换律是:______________________
向量加法的交换律是:______________________
结合律____________________________。
[小试身手、轻松过关]
3、对于零向量与任一向量 ,我们规定
,我们规定 +
+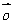 =___________=_______.
=___________=_______.
2、向量加法的平行四边形法则
以同一点O为起点的两个已知向量 ,
, (
(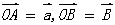 )为邻边作四边形OACB,则以O为起点对角线___________,就是
)为邻边作四边形OACB,则以O为起点对角线___________,就是 与
与 的和。这个法则就叫做两个向量求和的平行四边形法则。
的和。这个法则就叫做两个向量求和的平行四边形法则。
1、向量加法的三角形法则
:已知非零向量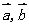 ,在平面内任取一点A,作
,在平面内任取一点A,作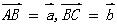 ,则向量__________叫做
,则向量__________叫做 与
与 的和,记作_____________,即
的和,记作_____________,即 =_______=__________这个法则就叫做向量求和的三角形法则。
=_______=__________这个法则就叫做向量求和的三角形法则。
1、判断下列命题的真假:
(1) 向量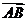 的长度和向量
的长度和向量 的长度相等.
的长度相等.
(2)向量 与
与 平行,则
平行,则 与
与 方向相同.
方向相同.
(3) 向量 与
与 平行,则
平行,则 与
与 方向相反.
方向相反.
(4) 两个有共同起点而长度相等的向量,它们的终点必相同.
(5) 若 与
与 平行同向,且
平行同向,且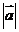 >
>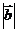 ,则
,则 >
>
(6)由于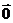 方向不确定,故
方向不确定,故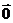 不能与任意向量平行。
不能与任意向量平行。
(7) 如果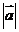 =
=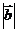 ,则
,则 与
与 长度相等。
长度相等。
(8) 如果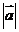 =
=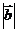 ,则与
,则与 与
与 的方向相同。
的方向相同。
(9) 若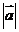 =
=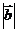 ,则
,则 与
与 的方向相反。
的方向相反。
(10)若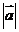 =
=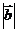 ,则与
,则与 与
与 的方向没有关系。
的方向没有关系。
[基础训练、锋芒初显]
11 请写出初中物理中的三个向量_________________________
12 关于零向量,下列说法中错误的是( )
A零向量是没有方向的。 B 零向量的长度是0
C 零向量与任一向量平行 D零向量的方向是任意的。
13 如果对于任意的向量 ,均有
,均有
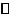
 ,则
,则 为_________________
为_________________
14 给出下列命题:
①向量的大小是实数 ② 平行响亮的方向一定相同 ③向量可以用有向线段表示 ④向量就是有向线段 正确的有_________________________
[举一反三、能力拓展]
15 把平行于某一直线的一切向量平移到同一起点,则这些向量的终点构成的图形是_________________________
16 把平面上的一切单位向量归结到共同的起点,那么这些向量的终点所构成的图形是_______________
[名师小结、感悟反思]
1 通过对既有大小,又有方向的一些量的认识,了解向量的实际背景。
2 掌握向量的表示法,可以用有向线段来表示向量,也可以用字母表示向量。用有向线段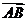 表示一个向量,显示了图形的直观性,为用向量处理几何问题和物理问题打下了基础。同时提供了一种几何方法,它也体现了数形结合的数学思想。另外,应该注意的是有向线段是向量的表示,并不是说向量就是有向线段。用字母表示向量便于向量运算。
表示一个向量,显示了图形的直观性,为用向量处理几何问题和物理问题打下了基础。同时提供了一种几何方法,它也体现了数形结合的数学思想。另外,应该注意的是有向线段是向量的表示,并不是说向量就是有向线段。用字母表示向量便于向量运算。
3 理解向量,零向量,单位向量,平行向量的概念。
因为向量即有大小,又有方向,所以向量不同于数量。数量之间可以比较大小,“大于”“小于”的概念对于数量是适用的。向量由模和方向确定,由于方向不能比较大小,因此“大于”“小于”对于向量来说是没有意义的,向量不能比较大小,向量的模可以比较大小。
任何一门数学分支,不管它如何抽象,总有一天会在现实世界的现象中找到应用。
§2.1.2 相等向量与共线向量
编者:刘凯
[学习目标、细解考纲]
1 理解相等向量与共线向量的概念
2 由向量相等的定义,理解平行向量与共线向量是等价的。
[知识梳理、双基再现]
1 相等向量是_________________________向量 与
与 相等,记作_______________。任意两个相等的非零向量,都可用一条有向线段来表示,并且与有向线段的___________无关。因为有向线段完全是由______________确定。 相反向量是_____________________。若
相等,记作_______________。任意两个相等的非零向量,都可用一条有向线段来表示,并且与有向线段的___________无关。因为有向线段完全是由______________确定。 相反向量是_____________________。若 与
与 是一对相反向量,则______________________
是一对相反向量,则______________________
2 共线向量
任一组平行向量都可以移动到同一直线上,因此_________________叫做共线向量,也就是说,共线向量的方向相同或相反。若 与
与 共线,即
共线,即 与
与 平行,记作
平行,记作


[小试身手、轻松过关]
1 如图,在矩形ABCD中,可以用一条有向线段表示的向量是( )
A  B
B
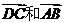 C
C 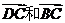 此处有图一
此处有图一
D 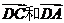
2 在△ABC中,DE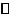 BC,则下列结论中正确的是
( )
BC,则下列结论中正确的是
( )
A  B
B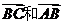 C
C 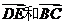
D  此处有图二
此处有图二
3 如图,设O是正六边形ABCDEF的中心,图中与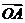 共线的向量有 ( )
共线的向量有 ( )
A 一个 B 两个 C三个 D四个 此处有图三
4下列命题中正确的是 ( )
A若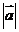 =
=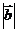 , 则
, 则 =
= B若
B若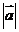 >
>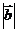 ,则
,则 >
>
C 若 =
= ,则
,则
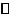
 D 若
D 若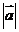 =1 ,则
=1 ,则 =1
=1
5 下列说法正确的有 ( )
Ⅰ 零向量比任何向量都小 Ⅱ零向量的方向是任意的 Ⅲ零向量与任一向量共线
Ⅳ零向量只能与零向量共线
A 0个 B 1个 C 2个 D 3个
6 平行四边形ABCD中,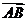 =
= 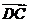 ,则相等的向量是( )
,则相等的向量是( )
A 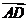 与
与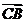 B
B 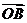 与
与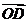 C
C 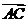 与
与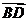 D
D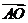 与
与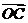
7 已知点O是正六边形ABCDEF的中心,则下列向量中含有相等向量的是( )
A  B
B  C
C 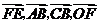
D 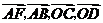
8 设O是正方形的中心,则向量 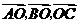 是 ( )
是 ( )
A有相同起点的向量 B 有相同终点的向量 C 相等的向量 D模相等的向量
9 若向量
 与向量
与向量 不相等,则
不相等,则  与
与 一定( )
一定( )
A 不共线 B 长度不相等 C 不都是单位向量 D 不都是零向量
10 如图,四边形PQRS是菱形,下列可用同一条有向线段表示的两个向量是( )
A 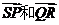 B
B 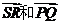 C
C  D
D 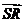 和
和
[基础训练、锋芒初显]
11 若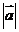 =2 ,
=2 , =
= ,则
,则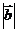 =___________________
=___________________ 的方向与
的方向与 _______。若
_______。若 = -
= - ,则
,则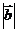 =____________,
=____________, 的方向与
的方向与 ___________
___________
12 如图所示,O是正方形ABCD的中心,图中与向量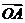 长度相等的向量有___________,与向量
长度相等的向量有___________,与向量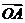 相等的向量有________,与
相等的向量有________,与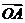 相反的向量有_____________
相反的向量有_____________
13 在正方形ABCD中,与向量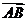 相等的向量有________,与
相等的向量有________,与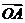 相反的向量有__________
相反的向量有__________
14 把所有相等的向量平移到同一个起点后,这些向量的终点将落在___________________
[举一反三、能力拓展]
15 O为正六边形ABCDEF的中心,分别写出与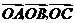 相等的向量。
相等的向量。
16 在一个平行四边形的边上,作出所有可能的向量,并求其相等向量的对数。
17 如图所示,四边形ABCD与ABDE都是平行四边形
(1)写出与向量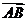 共线的向量。 (2)若
共线的向量。 (2)若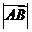 =2.5,求向量
=2.5,求向量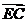 的模。
的模。
18 在直角坐标系中,画出向量 ,满足:①
,满足:① 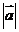 =5 ②
=5 ② 的方向与X轴正方向的夹角是
的方向与X轴正方向的夹角是
[名师小结、感悟反思]
1 由于零向量是特殊的向量,方向可看作是任意的 ,所以规定零向量与任意方向的向量平行。今后解答问题时,要注意看清题目中是“零向量”还是“非零向量”,从而正确解题。
2 零向量与零向量相等。任意两个相等的非零向量都可用一条有向线段来表示,并且与有向线段的起点无关。两个非零向量只有当它们的模相等,同时方向又相同时,才能称它们相等。例如 =
= ,就意味者
,就意味者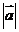 =
=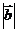 ,并且
,并且 与
与 的方向相同。
的方向相同。
3 共线向量也叫做平行向量,任一向量 都与它自身是平行向量(共线向量)。
都与它自身是平行向量(共线向量)。
§2 .2 平面向量的线性运算
§2.2.1向量的加法及其几何意义
编者:刘凯
[学习目标、细解考纲]
1 通过实际例子,掌握向量的加法运算,并理解向量加法的平行四边形法则和三角形法则则其几何意义。
2 灵活运用平行四边形法则和三角形法则进行向量求和运算。
3 通过本节学习,培养多角度思考问题的习惯,提高探索问题的能力。
[知识梳理、双基再现]
7、平行向量
_________________________叫做平行向量,向量 与
与 平行,通常记作______________
平行,通常记作______________
我们规定:零向量与任一向量平行,即对于任意的向量 ,都有_________________________.
,都有_________________________.
[小试身手、轻松过关]
6、单位向量是____________的向量.
5、零向量是_____________的向量,记作____________.零向量的方向任意.
4、向量的模的向量
向量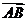 的大小,也就是向量
的大小,也就是向量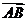 的长度,称_____________,记作__________.
的长度,称_____________,记作__________.
3、向量的几何表示
(1)由于实数与数轴上的点一一对应,所以数量常用_____________________表示,而且不同的点表示不同的数量.
(2)向量常用带箭头的线段表示,线段按一定比例(标度)画出,它的长短表示向量的____________,箭头的指向表示向量的________________.
(3)有象线段是________________的线段,通常在有向线段的终点处画上箭头表示它的方向.以A为起点,B为终点的有向线段记作____________.起点要写在终点的前面.
有向线段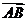 的长度,记作___________________.
的长度,记作___________________.
有向线段包含三个要素________________________________________________
知道了有向线段的起点,长度,和方向,它的终点就惟一确定.
(4)向量可以用有向线段表示.也可以用字母_________表示,或用表示向量的有向线段的起点和终点字母表示,例如字母_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com