
2、理解向量减法的几何意义,灵活进行向量的减法运算。
进行向量的减法运算
[知识梳理、双基再现]
1、在理解向量加法的基础上,掌握向量减法的运算及几何意义。
5、向量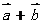 与向量
与向量 ,
, 的模及方向的关系。
的模及方向的关系。
①当两个非零向量 与
与 不共线时,
不共线时,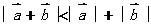 (由基角形法则可知),
(由基角形法则可知),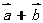 的方向与
的方向与 ,
, 都不相同。
都不相同。
②当 与
与 共线时,又同向与反向两种情况。当
共线时,又同向与反向两种情况。当 与
与 方向相同时,
方向相同时,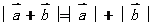 ,
,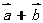 的方向与
的方向与 ,
, 都相同。
都相同。
当 与
与 方向相反时
方向相反时
若 ,则
,则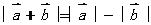
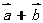 的方向与
的方向与 相同;
相同;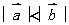 则
则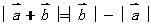
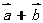 的方向与
的方向与 相同。
相同。
综上,可以得到性质。
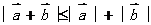
§2.2.2 向量减法运算及其几何意义
编者:刘凯
[学习目标、细解考纲]
4、向量加法的平行四边形法则与三角法则在本质上一致的,但当两个向量共线(平行)时,平行四边形法则就不适用了。
3、当两个向量共线(平行)时,三角形法则同样适用。
2、用向量加法的三角形法则作出两个向量的和,关键是掌握两个向量是首尾相连的,两个向量 与
与 相加,以
相加,以 的终点作为
的终点作为 的起点,则由
的起点,则由 的起点指向
的起点指向 的终点的有向线段就表示
的终点的有向线段就表示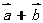 。即比如设
。即比如设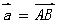 ,
,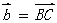 ,则
,则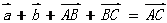 。
。
1、两个向量的加法的定义表明,两个向量的和仍是一个向量。
13、设 表示“向东走3km”
表示“向东走3km”  表示“向北走3km”则
表示“向北走3km”则 +
+ 表示什么意义?
表示什么意义?
[名师小结、感悟反思]
12、当向量 与
与 _______________________时,
_______________________时,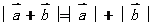
当向量 与
与 ________________________时,
________________________时,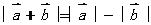
当向量 与
与 ________________________时,
________________________时,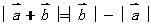
当向量 ,
, 不共线时,
不共线时,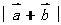 _______________
_______________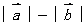 ,因此我们有
,因此我们有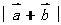 ______________
______________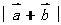 。
。
11、化简
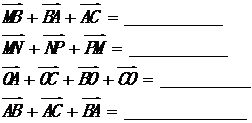
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com