1、在平面直角坐标系中，已知点A时坐标为(2，3)，点B的坐标为(6，5)，则=_______________，=__________________。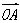

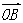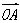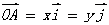4、以原点O为起点作向量，设，则向量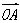，的坐标_____________，就是___________；反过来，终点A的坐标___________也就是__________________。

[小试身手、轻松过关]

3、几个特殊向量的坐标表示

2、向量的坐标表示

在平面直角坐标系中，分别取与x轴、y轴方向相同于两个_______作为基为基底。对于平面内的任一个向量，由平面向量基本定理可知，有且只有一对实数x，y使得____________，这样，平面内的任一向量都可由__________唯一确定，我们把有序数对________叫做向量的坐标，记作=___________此式叫做向量的坐标表示，其中x叫做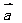在x轴上的坐标，y叫做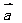在y轴上的坐标。

1、平面向量的正交分解

把一个向量分解为_____________，叫做把向量正交分解。

2、联系直角坐标系，研究向量正交分解的坐标运算。

[知识梳理、双基再现]

1、理解平面向量的正交分解。

3．由于零向量可看成与任何向量共线，所以零向量不可以作为基底。

§2．3.2　 平面向量的正交分解及坐标表示

编者：刘凯

[学习目标、细解考纲]

2．平面向量的基本定理中“同一平面内两个不共线的向量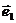、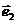”叫做基底，基底的条件是在同一平面内不共线，即同一平面内的两个向量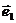、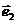只要不共线即可作为基底，换句话说，平面内向量的基底不唯一，那么同一平面内任何一组不共线的向量都可作为表示这一平面内的所有向量的基底。

1．平面向量的基本定理告诉我们，平面内任何一个向量都可以沿着两个不共线的方向分解成两个向量的和，并且这种分解是唯一的。