
6.向量的数量积满足下列运算律
已知向量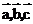 与实数
与实数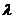 。
。
① =___________(______律)
=___________(______律)
②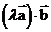 =___________
=___________
③ =___________
=___________
[小试身手、轻松过关]
5. 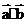 的几何意义:________________________________________。
的几何意义:________________________________________。
4.平面向量数量积的性质:设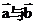 均为非空向量:
均为非空向量:
①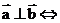 ___________
___________
②当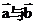 同向时,
同向时,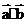 =________ 当
=________ 当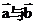 反向时,
反向时, =________,特别地,
=________,特别地, =__________或
=__________或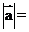 ___________。
___________。
③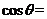 ___________
___________
④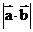 ______________
______________
3.零向量与任意向量的数量积为___________。
2.已知两个______向量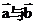 ,我们把______________叫
,我们把______________叫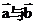 的数量积。(或________)记作___________即
的数量积。(或________)记作___________即 =______________________其中
=______________________其中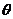 是
是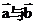 的夹角。______________________叫做向量
的夹角。______________________叫做向量 方向上的___________。
方向上的___________。
1._______________________________________叫做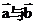 的夹角。
的夹角。
3.理解利用平面向量数量积,可以处理有关长度、角度和垂直问题。
[知识梳理、双基再现]
2.正确使用平面向量数量积的重要性质及运算律。
1.掌握平面向量数量积的意义;体会数量积与投影的关系。
2、向量的坐标表示,实际是向量的代数表示,在引入向量的坐标表示后,即可使向量运算完全代数化,将数与形紧密地结合起来了,这样,很多几何问题就转化为我们毫熟知的数量的运算。
§2.4平面向量的数量积
§2.4.1 平面向量的数量积
编者:曹惠民
[学习目标、细解考纲]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com