
2.已知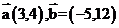 则
则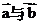 夹角的余弦为( )
夹角的余弦为( )
A. 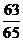 B.
B.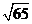 C.
C.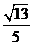 D.
D.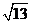
1.已知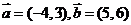 则
则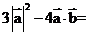 ( )
( )
A.23 B.57 C.63 D.83
4.两向量夹角的余弦(0≤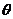 ≤
≤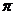 )
)
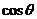 =__________________________________=_________________
=__________________________________=_________________
______________
如:已知A(1,0),B(3,1),C(-2,0),且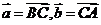 ,则
,则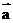 与
与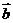 的夹角为_________________。
的夹角为_________________。
[小试身手、轻松过关]
3.向量垂直的判定
设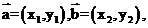 则
则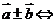 _________________
_________________
如:已知A(1,2), B(2,3), C(-2,5),求证 是直角三角形。
是直角三角形。
2.平面内两点间的距离公式
(1)设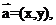 则
则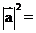 ________________或
________________或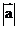 ________________。
________________。
(2)如果表示向量的有向线段的起点和终点的坐标分别为________________________________________________________________________________(平面内两点间的距离公式)
1. 平面向量数量积的坐标表示
已知两个非零向量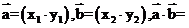 (坐标形式)。
(坐标形式)。
这就是说:(文字语言)两个向量的数量积等于 。
如:设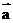 (5,-7),b=(-6,-4),求
(5,-7),b=(-6,-4),求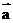
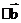 。
。
2.掌握向量垂直的坐标表示及夹角的坐标表示及平面向量点间的距离公式。
[知识梳理、双基再现]
1.掌握平面向量数量积的坐标表示,会进行平面向量数量积的坐标运算。
3.计算长度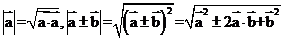
 求向量夹角
求向量夹角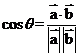
证明垂直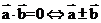 ,数量积三公式可解决长度、角度、垂直等问题
,数量积三公式可解决长度、角度、垂直等问题
§2.4.2 平面向量数量积的坐标表示 模 夹角
第一课时
编者:曹惠民
[学习目标、细解考纲]
2.向量的数量积不能是结合体。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com