
1、

[小试身手、轻松过关]
1、 经历用向量的数量积推导两角差的余弦公式的过程,体验和感受数学发现和创造的过程,体会向量和三角函数间的联系; 2、 用余弦的差角公式推出余弦的和角公式,理解化归思想在三角变换中的作用; 3、 能用余弦的和差角公式进行简单的三角函数式的化简、求值及恒等变形。
[知识梳理、双基再现]
15、已知向量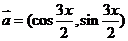 ,
,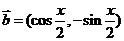 ,
, ,
,
(1)求证: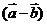 ⊥
⊥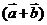 ; (2)
; (2) ,求
,求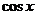 的值。(13分)
的值。(13分)
第三章 三角恒等变换
§3.1 两角和与差的正弦、余弦和正切公式
§3.1.1 两角和与差的余弦公式
编者:刘毅
[学习目标、细解考纲]
14、已知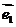 、
、 是夹角为60°的两个单位向量,
是夹角为60°的两个单位向量,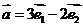 ,
,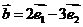
(1)求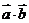 ;
(2)求
;
(2)求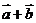 与
与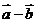 的夹角.
(12分)
的夹角.
(12分)
13、在直角△ABC中,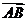 =(2,3),
=(2,3),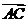 =(1,k),求实数k的值。(10分)
=(1,k),求实数k的值。(10分)
12、已知A(1,0),B(4,3),C(2,4),D(0,2),试证明四边形ABCD是梯形。(10分)
11、已知向量 与
与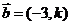 的夹角是钝角,则k的取值范围是
的夹角是钝角,则k的取值范围是
10、若A(-1,-2),B(4,8),C(5,x),且A、B、C三点共线,则x=
9、已知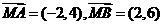 ,则
,则
8、已知
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com