
2. 掌握三角函数式的化简和证明的方法及步骤。
[知识梳理、双基再现]
1. 能正确运用三角公式,进行简单三角函数式的化简和恒等式证明(包括引出半角、积化和差、和差化积公式,但不要求记忆);
14.
已知 <
<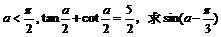 的值。
的值。
[名师小结、感悟反思]
三角函数式的求值的关键是熟练掌握公式及应用, 掌握公式的逆用和变形.
三角函数式的求值的类型一般可分为:
(1)“给角求值”:给出非特殊角求式子的值。仔细观察非特殊角的特点,找出和特殊角之间的关系,利用公式转化或消除非特殊角
(2)“给值求值”:给出一些角得三角函数式的值,求另外一些角得三角函数式的值。找出已知角与所求角之间的某种关系求解
(3)“给值求角”:转化为给值求值,由所得函数值结合角的范围求出角。
(4)“给式求值”:给出一些较复杂的三角式的值,求其他式子的值。将已知式或所求式进行化简,再求之
三角函数式常用化简方法:切割化弦、高次化低次
注意点:灵活角的变形和公式的变形
重视角的范围对三角函数值的影响,对角的范围要讨论
§3.2.2 三角函数化简及证明
编者:任传军
[学习目标 细解考纲]
13.已知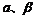 为锐角,
为锐角,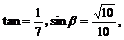 求a+2
求a+2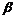 的值。
的值。
12.若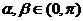 ,
,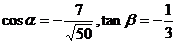 ,求α+2β。
,求α+2β。
[举一反三、能力拓展]
11. 已知tan(45°+θ)=3,求sin2θ-2cos2θ的值
10.已知a、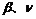 都是锐角,且
都是锐角,且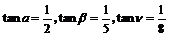 则a+
则a+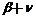 = 。
= 。
9.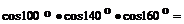 ;
;
8.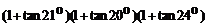 的值是( )
的值是( )
A.2 B.4 C.8 D.16
7.已知 是第三象限角,且
是第三象限角,且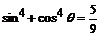 ,则
,则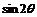 等于( )
等于( )
A.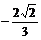 B.
B. 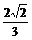 C.
C.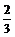 D.
D.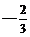
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com