
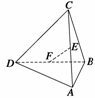
22.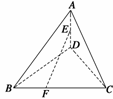 如图所示,在四面体ABCD中,E、F分别是线段AD、BC上的点,
如图所示,在四面体ABCD中,E、F分别是线段AD、BC上的点,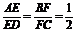 ,AB=CD=3,EF=
,AB=CD=3,EF=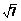 ,求AB、CD所成角的大小.
,求AB、CD所成角的大小.
解 如图所示,在线段BD上取一点G,使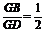 .连接GF、GE、EF.
.连接GF、GE、EF.
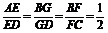 ,GE∥AB,
,GE∥AB, 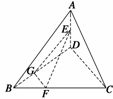 且GE=
且GE=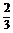 AB=2,
AB=2,
同理,GF∥CD,且GF= CD=1,
CD=1,
在△EGF中,cos∠EGF=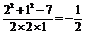 ,
,
∴∠EGF=120°.
由GF∥CD,GE∥AB可知,AB与CD所成的角应是∠EGF的补角为60°.
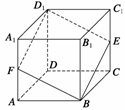
21.如图所示,在正方体ABCD-A1B1C1D1中,E、F分别为CC1、AA1的中点,画出平面BED1F与平面ABCD的交线.
解 在平面AA1D1D内, 延长D1F, ∵D1F与DA不平行,
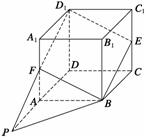 因此D1F与DA必相交于一点,设为P, 则P∈FD1,P∈DA. 又∵FD1
因此D1F与DA必相交于一点,设为P, 则P∈FD1,P∈DA. 又∵FD1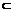 平面BED1F, AD
平面BED1F, AD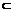 平面ABCD,
平面ABCD,
∴P∈平面BED1F, P∈平面ABCD.
又B为平面ABCD与平面BED1F的公共点连接PB,
∴PB即为平面BED1F与平面ABCD的交线.如图所示.
20.定线段AB所在的直线与定平面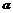 相交,P为直线AB外的一点,且P不在
相交,P为直线AB外的一点,且P不在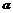 内,若直线AP、BP与
内,若直线AP、BP与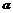 分别交于
分别交于
C、D点,求证:不论P在什么位置,直线CD必过一定点.
证明 设定线段AB所在直线为l,与平面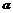 交于O点, 即l∩
交于O点, 即l∩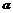 =O.
=O.
由题意可知,AP∩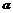 =C,BP∩
=C,BP∩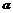 =D,∴C∈
=D,∴C∈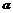 ,D∈
,D∈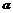 .
.
又∵AP∩BP=P,∴AP、BP可确定一平面 且C∈
且C∈ ,D∈
,D∈ . ∴CD=
. ∴CD=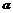 ∩
∩ .
.
∵A∈ ,B∈
,B∈ ,∴l
,∴l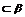 ,∴O∈
,∴O∈ .∴O∈
.∴O∈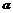 ∩
∩ ,即O∈CD.
,即O∈CD.
∴不论P在什么位置,直线CD必过一定点.
19.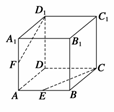 如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.
如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.
求证:(1)E,C,D1,F四点共面;(2)CE,D1F,DA三线共点.
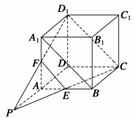
证明 (1)如图所示,连接CD1,EF,A1B, ∵E、F分别是AB和AA1的中点,
∴EF∥A1B且EF= A1B, 又∵A1D1
A1B, 又∵A1D1 BC∴四边形A1BCD1是平行四边形,
BC∴四边形A1BCD1是平行四边形,
 ∴A1B∥CD1,∴EF∥CD1, ∴EF与CD1确定一个平面
∴A1B∥CD1,∴EF∥CD1, ∴EF与CD1确定一个平面 ,
,
∴E,F,C,D1∈ , 即E,C,D1,F四点共面.
, 即E,C,D1,F四点共面.
(2)由(1)知EF∥CD1,且EF= CD1, ∴四边形CD1FE是梯形,
CD1, ∴四边形CD1FE是梯形,
∴CE与D1F必相交,设交点为P, 则P∈CE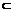 平面ABCD,
平面ABCD,
且P∈D1F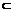 平面A1ADD1, ∴P∈平面ABCD且P∈平面A1ADD1.
平面A1ADD1, ∴P∈平面ABCD且P∈平面A1ADD1.
又平面ABCD∩平面A1ADD1=AD, ∴P∈AD,∴CE,D1F,DA三线共点.
17.已知a、b为不垂直的异面直线,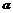 是一个平面,则a、b在
是一个平面,则a、b在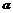 上的射影可能是
上的射影可能是
①两条平行直线; ②两条互相垂直的直线; ③同一条直线;④一条直线及其外一点.
则在上面的结论中,正确结论的编号是 ①②④ (写出所有正确结论的编号).
18用图形表示:a∩b=m,aÌa,bÌb,
a∩m=A,b∩m=B,c∩a=P,PÏa,cËb.
16.如图所示,在三棱锥C-ABD中,E、F分别是AC和BD的中点,若CD=2AB=4,EF⊥AB,则EF与 CD所成的角是30° .
15. 在棱长为
在棱长为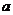 的正四面体中,相对两条棱间的距离为__________.
的正四面体中,相对两条棱间的距离为__________.
14.已知a∥c,b与c不平行、 a与b不相交,a,b的位置关系是
13.互不重合的三个平面的交线可能有__________条.
12. (2009·青岛调研)如图所示,在正三角形ABC中,D、E、F分别为各边的中点,G、H、I、J分别为AF、AD、BE、DE的中点,将△ABC沿DE、EF、DF折成三棱锥以后,GH与IJ所成角的度数为 (
)
(2009·青岛调研)如图所示,在正三角形ABC中,D、E、F分别为各边的中点,G、H、I、J分别为AF、AD、BE、DE的中点,将△ABC沿DE、EF、DF折成三棱锥以后,GH与IJ所成角的度数为 (
)
? A.90°?? B.60°? C.45°? D.0°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com