
3.(2008·长沙模拟)对于不重合的两个平面 与
与 ,给定下列条件:
,给定下列条件:
①存在平面 ,使得
,使得 ,
, 都垂直于
都垂直于 ; ②存在平面
; ②存在平面 ,使得
,使得 ,
, 都平行于
都平行于 ; ③存在直线l
; ③存在直线l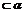 ,直线m
,直线m ,使得l∥m; ④存在异面直线l、m,使得l∥
,使得l∥m; ④存在异面直线l、m,使得l∥ ,l∥
,l∥ ,m∥
,m∥ ,m∥
,m∥ . 其中,可以判定
. 其中,可以判定 与
与 平行的条件有( B ) A.1个 ? B.2个? C.3个? D.4个
平行的条件有( B ) A.1个 ? B.2个? C.3个? D.4个
2.平面 ∥平面
∥平面 的一个充分条件是 ( D )
的一个充分条件是 ( D )
?A.存在一条直线a,a∥ ,a∥
,a∥ ?B.存在一条直线a,a
?B.存在一条直线a,a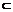
 ,a∥
,a∥
?C.存在两条平行直线a,b,a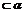 ,b
,b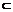
 ,a∥
,a∥ ,b∥
,b∥ D.存在两条异面直线a,b,a
D.存在两条异面直线a,b,a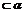 ,b
,b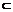
 ,a∥
,a∥ ,b∥
,b∥
1.下列命题,其中真命题的个数为 ( A )
①直线l平行于平面 内的无数条直线,则l∥
内的无数条直线,则l∥ ;②若直线a在平面
;②若直线a在平面 外,则a∥
外,则a∥ ; ③若直线a∥b,直线b
; ③若直线a∥b,直线b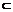
 ,则a∥
,则a∥ ; ④若直线a∥b,b
; ④若直线a∥b,b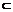
 ,那么直线a就平行于平面
,那么直线a就平行于平面 内的无数条直线.
内的无数条直线.
?A.1 ? B.2 ? C.3 ? D.4
例1.如图所示,空间四边形ABCD中,E、F、G分别在AB、BC、CD上,且满足AE∶EB=CF∶FB=2∶1,
CG∶GD=3∶1,过E、F、G的平面交AD于H,连接EH. (1)求AH∶HD;(2)求证:EH、FG、BD三线共点.
 (1)解 ∵
(1)解 ∵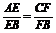 =2,∴EF∥AC. ∴EF∥平面ACD.而EF
=2,∴EF∥AC. ∴EF∥平面ACD.而EF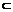 平面EFGH, 且平面EFGH∩平面ACD=GH, ∴EF∥GH.而EF∥AC, ∴AC∥GH. ∴
平面EFGH, 且平面EFGH∩平面ACD=GH, ∴EF∥GH.而EF∥AC, ∴AC∥GH. ∴ =3,即AH∶HD=3∶1.
=3,即AH∶HD=3∶1.
(2)证明 ∵EF∥GH,且 ,
, , ∴EF≠GH,∴四边形EFGH为梯形.
, ∴EF≠GH,∴四边形EFGH为梯形.
令EH∩FG=P,则P∈EH,而EH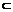 平面ABD, P∈FG,FG
平面ABD, P∈FG,FG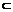 平面BCD,平面ABD∩平面BCD=BD,
平面BCD,平面ABD∩平面BCD=BD,
∴P∈BD.∴EH、FG、BD三线共点.
 例2 如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1,B1C1的中点.问:
例2 如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1,B1C1的中点.问:
(1)AM和CN是否是异面直线?说明理由; (2)D1B和CC1是否是异面直线?说明理由.
解 (1)不是异面直线.理由如下:

 ∵M、N分别是A1B1、B1C1的中点.∴MN∥A1C1, 又∵A1A D1D,而D1D C1C,
∵M、N分别是A1B1、B1C1的中点.∴MN∥A1C1, 又∵A1A D1D,而D1D C1C,
 ∴A1A CC1,∴四边形A1ACC1为平行四边形.
∴A1A CC1,∴四边形A1ACC1为平行四边形.
∴A1C1∥AC,得到MN∥AC, ∴A、M、N、C在同一个平面内,故AM和CN不是异面直线.
(2)是异面直线.证明如下:
假设D1B与CC1在同一个平面D1CC1内,则B∈平面CC1D1,C∈平面CC1D1.
∴BC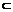 平面CC1D1,这与在正方体中BC⊥平面CC1D1相矛盾,∴假设不成立,故D1B与CC1是异面直线.
平面CC1D1,这与在正方体中BC⊥平面CC1D1相矛盾,∴假设不成立,故D1B与CC1是异面直线.
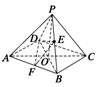
例 3在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.若E是PB的中点,求异面直线DE与PA所成角的余弦值.
3在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.若E是PB的中点,求异面直线DE与PA所成角的余弦值.
解 取AB的中点F,连接EF,DF, ∵E为PB中点,∴EF∥PA,
∴∠DEF为异面直线DE与PA所成角(或其补角).在Rt△POB中,∵BO=AB·sin30°=1,
又PO⊥OB,∴PO=BO·tan60°= . 在Rt△AOB中,AO=AB·cos30°=
. 在Rt△AOB中,AO=AB·cos30°= =OP,
=OP,
 ∴在Rt△POA中,PA=
∴在Rt△POA中,PA= ,∴EF=
,∴EF=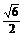 . 在正三角形ABD和正三角形PDB中,DF=DE=
. 在正三角形ABD和正三角形PDB中,DF=DE= ,
,
由余弦定理得 ∴cos∠DEF=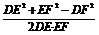 =
= .
.
 所以异面直线DE与PA所成角的余弦值为
所以异面直线DE与PA所成角的余弦值为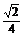 .
.
例4.如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,且EH与FG相交于点O. 求证:B、D、O三点共线. 证明 ∵E∈AB,H∈AD, ∴E∈平面ABD,H∈平面ABD.
∴EH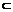 平面ABD. ∵EH∩FG=O,∴O∈平面ABD. 同理可证O∈平面BCD,
平面ABD. ∵EH∩FG=O,∴O∈平面ABD. 同理可证O∈平面BCD,
∴O∈平面ABD∩平面BCD,即O∈BD, 所以B、D、O三点共线.
 例5.在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG. 求证:直线FG
例5.在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG. 求证:直线FG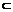 平面ABCD且直线FG∥直线A1B1.
平面ABCD且直线FG∥直线A1B1.
证明 由已知得E是CD的中点,在正方体中,由于A∈平面ABCD, E∈平面ABCD,
所以AE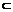 平面ABCD. 又AE∩BC=F, 从而F∈平面ABCD.
平面ABCD. 又AE∩BC=F, 从而F∈平面ABCD.
 同理G∈平面ABCD,所以FG
同理G∈平面ABCD,所以FG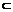 平面ABCD.因为EC
平面ABCD.因为EC 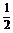 AB,故在Rt△FBA中,CF=BC,同理DG=AD.
AB,故在Rt△FBA中,CF=BC,同理DG=AD.

 又在正方形ABCD中,BC AD,所以CF DG,所以四边形CFGD是平行四边形,
又在正方形ABCD中,BC AD,所以CF DG,所以四边形CFGD是平行四边形,
所以FG∥CD.又CD∥AB,AB∥A1B1, 所以直线FG∥直线A1B1.
4.下列各图是正方体或正四面体,P、Q、R、S分别是所在棱的中点,则PQ与SR一定是异面直线的是
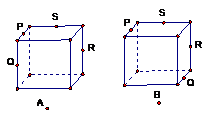

3. 直线a、b相交于点O且a、b成60°角,过点O与a、b都成60°角的直线有( )
2. 对平面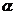 和共面的直线
和共面的直线 下列命题中真命题是
( )
下列命题中真命题是
( )
(A)若 则
则 (B)若
(B)若 则
则
(C)若 则
则 (D)若
(D)若 与
与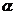 所成的角相等,则
所成的角相等,则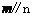
1.共点的四条直线最多可以确定_______平面;互不相交的三条直线可以确定_______平面.
例1.如图所示,空间四边形ABCD中,E、F、G分别在AB、BC、CD上,且满足AE∶EB=CF∶FB=2∶1,
CG∶GD=3∶1,过E、F、G的平面交AD于H,连接EH. (1)求AH∶HD;(2)求证:EH、FG、BD三线共点.
 例2 如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1,B1C1的中点.问:
例2 如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1,B1C1的中点.问:
(1)AM和CN是否是异面直线?说明理由; (2)D1B和CC1是否是异面直线?说明理由.
例 3在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.若E是PB的中点,求异面直线DE与PA所成角的余弦值.
3在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.若E是PB的中点,求异面直线DE与PA所成角的余弦值.
 例4.如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,且EH与FG相交于点O. 求证:B、D、O三点共线.
例4.如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,且EH与FG相交于点O. 求证:B、D、O三点共线.
例5.在正方体AC1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG. 求证:直线FG 平面ABCD且直线FG∥直线A1B1.
平面ABCD且直线FG∥直线A1B1.
22. 如图所示,在四面体ABCD中,E、F分别是线段AD、BC上的点,
如图所示,在四面体ABCD中,E、F分别是线段AD、BC上的点, ,AB=CD=3,EF=
,AB=CD=3,EF=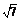 ,求AB、CD所成角的大小.
,求AB、CD所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com