
7.已知直线 和平面
和平面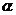 ,则
,则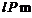 的一个充分但不必要的条件是( )
的一个充分但不必要的条件是( )
A.  与
与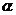 成等角 B.
成等角 B.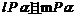 C.
C. 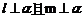 D.
D. 
6.给出下列关于互不相同的直线m,l,n和平面 ,
, 的四个命题:
的四个命题:
①若m ,l∩
,l∩ =A,点A
=A,点A m,则l与m不共面;②若m,l是异面直线,l∥
m,则l与m不共面;②若m,l是异面直线,l∥ ,m∥
,m∥ ,且n⊥l,n⊥m,则n⊥
,且n⊥l,n⊥m,则n⊥ ;③若l∥
;③若l∥ ,m∥
,m∥ ,
, ∥
∥ ,则l∥m; ④若l
,则l∥m; ④若l ,m
,m ,l∩m=A,l∥
,l∩m=A,l∥ ,m∥
,m∥ ,则
,则 ∥
∥ . 其中为假命题的是( ) A.①? B.②? C.③ D.④
. 其中为假命题的是( ) A.①? B.②? C.③ D.④
5.(2008·湖南理,5)设有直线m、n和平面 、
、 .下列四个命题中,正确的是 ( )
.下列四个命题中,正确的是 ( )
?A.若m∥ ,n∥
,n∥ ,则m∥n? B.若m
,则m∥n? B.若m ,n
,n ,m∥
,m∥ ,n∥
,n∥ ,则
,则 ∥
∥
?C.若 ⊥
⊥ ,m
,m ,则m⊥
,则m⊥ ? D.若
? D.若 ⊥
⊥ ,m⊥
,m⊥ ,m
,m ,则m∥
,则m∥
4.(2008·海南,宁夏文,12)已知平面 ⊥平面
⊥平面 ,
, ∩
∩ =l,点A∈
=l,点A∈ ,A
,A l,直线AB∥l,直线AC⊥l,直线m∥
l,直线AB∥l,直线AC⊥l,直线m∥ ,m∥
,m∥ ,则下列四种位置关系中,不一定成立的是 ( )
,则下列四种位置关系中,不一定成立的是 ( )
?A.AB∥m? B.AC⊥m? C.AB∥ ? D.AC⊥
? D.AC⊥
3.(2008·长沙模拟)对于不重合的两个平面 与
与 ,给定下列条件:
,给定下列条件:
①存在平面 ,使得
,使得 ,
, 都垂直于
都垂直于 ; ②存在平面
; ②存在平面 ,使得
,使得 ,
, 都平行于
都平行于 ; ③存在直线l
; ③存在直线l ,直线m
,直线m ,使得l∥m; ④存在异面直线l、m,使得l∥
,使得l∥m; ④存在异面直线l、m,使得l∥ ,l∥
,l∥ ,m∥
,m∥ ,m∥
,m∥ . 其中,可以判定
. 其中,可以判定 与
与 平行的条件有( ) A.1个 ? B.2个? C.3个? D.4个
平行的条件有( ) A.1个 ? B.2个? C.3个? D.4个
2.平面 ∥平面
∥平面 的一个充分条件是 (
)
的一个充分条件是 (
)
?A.存在一条直线a,a∥ ,a∥
,a∥ ?B.存在一条直线a,a
?B.存在一条直线a,a
 ,a∥
,a∥
?C.存在两条平行直线a,b,a ,b
,b
 ,a∥
,a∥ ,b∥
,b∥ D.存在两条异面直线a,b,a
D.存在两条异面直线a,b,a ,b
,b
 ,a∥
,a∥ ,b∥
,b∥
1.下列命题,其中真命题的个数为 ( )
①直线l平行于平面 内的无数条直线,则l∥
内的无数条直线,则l∥ ;②若直线a在平面
;②若直线a在平面 外,则a∥
外,则a∥ ; ③若直线a∥b,直线b
; ③若直线a∥b,直线b
 ,则a∥
,则a∥ ; ④若直线a∥b,b
; ④若直线a∥b,b
 ,那么直线a就平行于平面
,那么直线a就平行于平面 内的无数条直线.
内的无数条直线.
?A.1 ? B.2 ? C.3 ? D.4
16.如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.
 解 SG∥平面DEF.证明如下:连接CG交DE于点H,∵DE是△ABC的中位线, ∴DE∥AB.
解 SG∥平面DEF.证明如下:连接CG交DE于点H,∵DE是△ABC的中位线, ∴DE∥AB.
在△ACG中,D是AC的中点,且DH∥AG.
∴H为CG的中点. ∴FH是△SCG的中位线, ∴FH∥SG.
又SG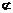 平面DEF,FH
平面DEF,FH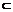 平面DEF, ∴SG∥平面DEF.
平面DEF, ∴SG∥平面DEF.
15.如图所示,正四棱锥P-ABCD的各棱长均为13,M,N分别为PA,BD上的点,且PM∶MA=BN∶ND=5∶8.
(1)求证:直线MN∥平面PBC; 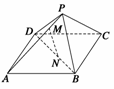 (2)求线段MN的长.
(2)求线段MN的长.
(1)证明 连接AN并延长交BC于Q,连接PQ,
∵AD∥BQ,∴△AND∽△QNB, ∴
又∵ ∴
∴ ∴MN∥PQ,
∴MN∥PQ,
又∵PQ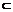 平面PBC, MN
平面PBC, MN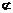 平面PBC, ∴MN∥平面PBC.
平面PBC, ∴MN∥平面PBC.
(2)解 在等边△PBC中,∠PBC=60°, 在△PBQ中由余弦定理知
PQ2 = PB2+BQ2-2PB·BQcos∠PBQ = 132+ -2×13×
-2×13×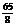 ×
×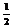 =
=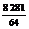 , ∴PQ=
, ∴PQ= ,
,
∵MN∥PQ,MN∶PQ=8∶13, ∴MN= =7.
=7.
14. 如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.设E是DC的中点,求证:D1E∥平面A1BD.证明 连结BE,则四边形DABE为正方形,∴BE=AD=A1D1, 且BE∥AD∥A1D1,
如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.设E是DC的中点,求证:D1E∥平面A1BD.证明 连结BE,则四边形DABE为正方形,∴BE=AD=A1D1, 且BE∥AD∥A1D1,
∴四边形A1D1EB为平行四边形.
∴D1E∥A1B.
又D1E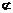 平面A1BD,
平面A1BD,
A1B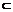 平面A1BD,
平面A1BD,
∴D1E∥平面A1BD.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com