
5.(2008·安徽理,4)已知m、n是两条不同直线, 、
、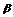 、
、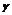 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
?A.若m∥ ,n∥
,n∥ ,则m∥n B.若
,则m∥n B.若 ⊥
⊥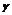 ,
,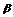 ⊥
⊥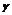 ,则
,则 ∥
∥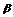
?C.若m∥ ,m∥
,m∥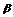 ,则
,则 ∥
∥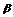 D.若m⊥
D.若m⊥ ,n⊥
,n⊥ ,则m∥n
,则m∥n
4.平面 的斜线AB交
的斜线AB交 于点B,过定点A的动直线l与AB垂直,且交
于点B,过定点A的动直线l与AB垂直,且交 于点C,则动点C的轨迹是 ( )
于点C,则动点C的轨迹是 ( )
?A.一条直线 ?B.一个圆 ?C.一个椭圆 D.双曲线的一支
3.已知m、n是两条不重合的直线, 、
、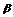 是两个不重合的平面,下列命题中正确的是 ( )
是两个不重合的平面,下列命题中正确的是 ( )
?A.若m∥ ,n∥
,n∥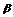 ,
,  ∥
∥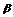 ,则m∥n B.若m∥n,n
,则m∥n B.若m∥n,n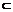
 ,m
,m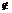
 ,则m∥
,则m∥
?C.若 ⊥
⊥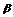 ,m⊥
,m⊥ ,则m∥
,则m∥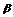 ? D.若m⊥
? D.若m⊥ ,n
,n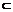
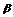 ,m⊥n,则
,m⊥n,则 ⊥
⊥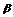
2.给定空间中的直线l及平面 .条件“直线l与平面
.条件“直线l与平面 内无数条直线都垂直”是“直线l与平面
内无数条直线都垂直”是“直线l与平面 垂直”的( )
垂直”的( )
?A.充要条件? B.充分非必要条件?C.必要非充分条件 ? D.既非充分又非必要条件
1.下面命题中:①两平面相交,如果所成的二面角是直角,则这两个平面垂直;②一个平面经过另一个平面的一条垂线,则这两个平面一定垂直;③一直线与两平面中的一个平行与另一个垂直,则这两个平面垂直;④一平面与两平行平面中的一个垂直,则与另一个平面也垂直;⑤两平面垂直,经过第一个平面上一点垂直于它们交线的直线必垂直于第二个平面. 其中正确的命题有 ( )
?A.2个? B.3个? C.4个? D.5个
17.(08山东文)如图,在四棱锥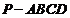 中,平面
中,平面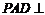 平面
平面 ,
,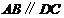 ,
,

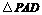 是等边三角形,已知
是等边三角形,已知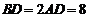 ,
,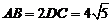 .(Ⅰ)设
.(Ⅰ)设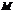 是
是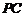 上的一点,证明:平面
上的一点,证明:平面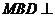 平面
平面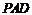 ;(Ⅱ)略.
;(Ⅱ)略.
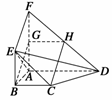
16.如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,

 ∠BAD=∠FAB=90°,BC
∠BAD=∠FAB=90°,BC 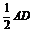 ,BE
,BE 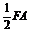 ,G、H分别为FA、FD的中点. (1)证明:四边形BCHG是平行四边形; (2)C、D、F、E四点是否共面?为什么? (3)设AB=BE,证明:平面ADE⊥平面CDE.
,G、H分别为FA、FD的中点. (1)证明:四边形BCHG是平行四边形; (2)C、D、F、E四点是否共面?为什么? (3)设AB=BE,证明:平面ADE⊥平面CDE.

 解 (1)由题设知,FG=GA, FH=HD,所以GH
解 (1)由题设知,FG=GA, FH=HD,所以GH 
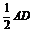 .又BC
.又BC 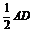 ,故GH BC
,故GH BC
 所以四边形BCHG是平行四边形.
所以四边形BCHG是平行四边形.
(2)C、D、F、E四点共面.理由如下:

 由BE
由BE 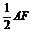 ,G是FA的中点知, BE GF,所以EF∥BG.
,G是FA的中点知, BE GF,所以EF∥BG.
由(1)知BG∥CH,所以EF∥CH,故EC、FH共面.
又点D在直线FH上,所以C、D、F、E四点共面.
 (3)如图(1),连接EG,由AB=BE,BE AG及∠BAG=90°知ABEG是正方形,故BG⊥EA.
(3)如图(1),连接EG,由AB=BE,BE AG及∠BAG=90°知ABEG是正方形,故BG⊥EA.
由题设知,FA、AD、AB两两垂直,故AD⊥平面FABE,
因此EA是ED在平面FABE内的射影,根据三垂线定理,BG⊥ED.
又ED∩EA=E,所以BG⊥平面ADE. 由(1)知,CH∥BG,所以CH⊥平面ADE.
由(2)知CH 平面CDE,得平面ADE⊥平面CDE.
平面CDE,得平面ADE⊥平面CDE.
15.如图所示,在三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点.
(1)证明:平面PBE⊥平面PAC; (2)如何在BC上找一点F,使AD∥平面PEF?并说明理由.
(1)证明 因为PA⊥底面ABC,所以PA⊥BE. 又因为△ABC是正三角形,且E为AC的中点, 所以BE⊥CA.
 又PA∩CA=A,所以BE⊥平面PAC. 因为BE
又PA∩CA=A,所以BE⊥平面PAC. 因为BE 平面PBE,所以平面PBE⊥平面PAC.
平面PBE,所以平面PBE⊥平面PAC.
(2)解 取CD的中点F,则点F即为所求.如图,连结EF,
因为E、F分别为CA、CD的中点, 所以EF∥AD.
又EF 平面PEF,AD
平面PEF,AD 平面PEF, 所以AD∥平面PEF.
平面PEF, 所以AD∥平面PEF.
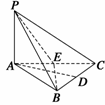
14. 四面体ABCD中,AC=BD,E、F分别是AD、BC的中点,且EF=
四面体ABCD中,AC=BD,E、F分别是AD、BC的中点,且EF=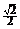 AC,∠BDC=90°.
AC,∠BDC=90°.
求证:BD⊥平面ACD.
证明 如图所示,取CD的中点G,连接EG、FG、EF.∵E、F分别为AD、BC的中点,

 ∴EG
∴EG 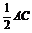 ,FG
,FG 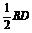 . 又AC=BD,∴EG=FG=
. 又AC=BD,∴EG=FG=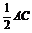 .
.
∴在△EFG中,EG2+FG2=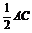 2=EF2. ∴EG⊥FG.∴BD⊥AC.
2=EF2. ∴EG⊥FG.∴BD⊥AC.
又∠BDC=90°,即BD⊥CD,AC∩CD=C, ∴BD⊥平面ACD.
13.四棱锥P-ABCD的底面ABCD是边长为a的正方形, PA=a,PB=PD= a,则它的5个面中,互相垂直的面有5 对.
a,则它的5个面中,互相垂直的面有5 对.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com