2.如果直线l⊥平面a，①若直线m⊥l,则m∥a；　 ②若m⊥a,则m∥l；③若m∥a,则m⊥l； ④若m∥l,则m⊥a,

上述判断正确的是　　　　　　　　　　　　　　　　　　 (　 )

A.①②③　　　 B.②③④　　 C.①③④　　　 D.②④

1.已知a，b，c是直线，a，b是平面，下列条件中，能得出直线a⊥平面a的是(　 )

A.a⊥c,a⊥b，其中bÌa,cÌa　　　 B.a⊥b,b∥a　　　 　C.a⊥b，a∥b　　　　　 D.a∥b,b⊥a

6．三垂线定理：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

三垂线定理的逆定理：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

双双基题目练练手

5.斜线、射影、直线和平面所成的角：定义--

性质：从平面外一点向平面所引的垂线段和斜线段中

(1)　　　　　　 最短；(2)斜线段相等<=>　　　　　 ；(3)斜线段较长(短)<=>　　　　　　　　 .

4．面面垂直的性质: 如果两个平面垂直，　　　　　　　　　 垂直于交线的直线也垂直于另一个平面。

3..线面垂直的性质：

①若一条直线垂直一个平面，则这条直线　　　　　 平面内所有直线；②垂直于同一个平面的两条直线　　　　　 .③垂直于同一直线的两平面　　　　　 。

2.面面垂直的证明：①计算二面角的平面角为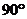 ；②如果一个平面　　　　　　　　 一条垂线,那么这两个平面垂直;

1.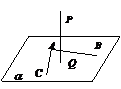线面垂直的判定：①判定定理；　　　　　　　　　　　　　　　　　　　　 ，②如果两条平行线中一条垂直于一个平面,那么　　　　　　　　 这个平面；③一条直线垂直于两个平行平面中的一个平面,它　　　　　　　　　　　 ；④两个平面垂直,　　　　　　　　　　　　　　　　　　 垂直于另一个平面.⑤如果两个相交平面都与第三个平面垂直,那么　　　　　　　 与第三个平面垂直.　　　　　　　　　　　

⑥向量法：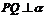

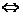
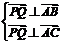
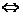
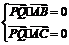
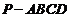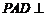17.(08山东文)如图，在四棱锥中，平面平面，，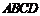

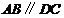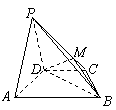
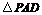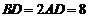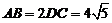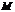是等边三角形，已知，．(Ⅰ)设是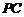上的一点，证明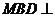：平面平面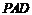；(Ⅱ)略．

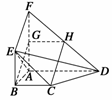
16.如图所示，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠FAB=90°,BC　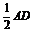 ，BE　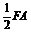 ，G、H分别为FA、FD的中点.　(1)证明：四边形BCHG是平行四边形；　(2)C、D、F、E四点是否共面？为什么？　(3)设AB=BE，证明：平面ADE⊥平面CDE.