1.已知a，b，c是直线，a，b是平面，下列条件中，能得出直线a⊥平面a的是(　 )

A.a⊥c,a⊥b，其中bÌa,cÌa　　　 B.a⊥b,b∥a　　　 　C.a⊥b，a∥b　　　　　 D.a∥b,b⊥a

6．三垂线定理：平面内的直线，如果和这个平面的一条斜线的射影垂直，那么它也和斜线垂直。

三垂线定理的逆定理：平面内的直线，如果和这个平面的一条斜线垂直，那麽它也和这条斜线的射影垂直

双双基题目练练手

5.斜线、射影、直线和平面所成的角：定义--

性质：从平面外一点向平面所引的垂线段和斜线段中

(1)垂线段最短；(2)斜线段相等<=>射影相等；(3)斜线段较长(短)<=>射影较长(短).

4．面面垂直的性质: 如果两个平面垂直，在一个平面内垂直于交线的直线也垂直于另一个平面。

3..线面垂直的性质：

①若一条直线垂直一个平面，则这条直线垂直于平面内所有直线；②垂直于同一个平面的两条直线平行.③垂直于同一直线的两平面平行。

2.面面垂直的证明：①计算二面角的平面角为 ；②如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直;

1.线面垂直的判定：

①判定定理；②如果两条平行线中一条垂直于一个平面,那么另一条也垂直于这个平面；③一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面；④两个平面垂直,在一个平面内垂直于它们交线的直线垂直于另一个平面.⑤如果两个相交平面都与第三个平面垂直,那么它们的交线与第三个平面垂直.　　　　　　　　　　　

⑥向量法：

5．(2006浙江)正四面体ABCD的棱长为l，棱AB∥平面，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是　　　　　　　　　　

典例剖析

例1已知PA⊥矩形ABCD所在平面，M，N分别是AB，PC的中点.①求证：MN⊥CD；②若∠PDA=45°求证：MN⊥平面PCD.　

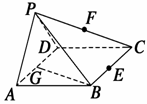例2　 如图所示，在四棱锥P-ABCD中，底面ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD，若G为AD边的中点，(1)求证：BG⊥平面PAD；　(2)求证：AD⊥PB；(3)若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD，并证明你的结论.　

例3如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°,PA=AB=BC,E是PC的中点.证明：　

(1)CD⊥AE；(2)PD⊥平面ABE.　

例4　 如图所示，直三棱柱ABC-A₁B₁C₁中，B₁C₁=A₁C₁， AC₁⊥A₁B，M、N分别是A₁B₁、AB的中点.　

(1)求证：C₁M⊥平面A₁ABB₁；　(2)求证：A₁B⊥AM；(3)求证：平面AMC₁∥平面NB₁C；(4)求A₁B与B₁C所成的角.　

4.已知P为Rt△ABC所在平面外一点，且PA=PB=PC，D为斜边AB的中点，则直线PD与平面ABC.　　　 (　 )

A．垂直　　　 B.斜交　　 C.成600角　　 D.与两直角边长有关

3.直角△ABC的斜边BC在平面a内，顶点A在平面a外，则△ABC的两条直角边在平面a内的射影与斜边BC组成的图形只能是　　　　　　　　　 (　 )

A.一条线段　　　 B.一个锐角三角形　 C.一个钝角三角形　 D.一条线段或一个钝角三角形