
6.A、B、C、D是空间不共面的四点,且满足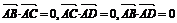 ,则△BCD是 ( B )
,则△BCD是 ( B )
?A.钝角三角形 B.锐角三角形 ?C.直角三角形 D.不确定
5.已知A(4,1,3),B(2,-5,1),C为线段AB上一点,且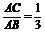 ,则C点的坐标为( C ) A.
,则C点的坐标为( C ) A.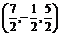 ? B.
? B.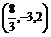 ?C.
?C.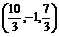 D.
D.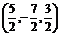
4.已知空间四边形ABCD的每条边和对角线的长都等于a,点E、F分别是BC、AD的中点,则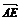 ·
·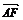 的值为( C )
的值为( C )
?A.a2? B.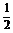 a2? C.
a2? C.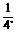 a2 ? D.
a2 ? D.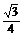 a2
a2
3.(2009·东莞模拟)已知向量a,b满足|a|=2,|b|=3,|2a+b|=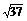 ,则a与b的夹角为 ( C ) A.30° B.45°? C.60° D.90°?
,则a与b的夹角为 ( C ) A.30° B.45°? C.60° D.90°?
2.已知向量a=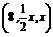 ,b=(x,1,2),其中x>0.若a∥b,则x的值为 ( B ) A.8? B.4 ? C.2? D.0
,b=(x,1,2),其中x>0.若a∥b,则x的值为 ( B ) A.8? B.4 ? C.2? D.0
1.已知点O、A、B、C为空间不共面的四点,且向量a=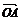 +
+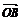 +
+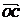 ,向量b=
,向量b=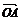 +
+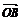 -
-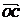 ,则与a,b不能构成空间基底的向量是 (
C )
,则与a,b不能构成空间基底的向量是 (
C )
A.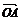 ? B.
? B.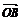 ? C.
? C.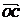 ? D.
? D.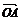 或
或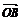
5.(2006浙江)正四面体ABCD的棱长为l,棱AB∥平面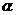 ,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是______.
,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是______.
◆答案提示:1-3.DBDA; 5. 6. 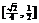 .CD⊥平面α时射影面积最小
.CD⊥平面α时射影面积最小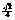 ;CD//α时射影面积最大
;CD//α时射影面积最大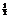 .
.
 典例剖析
典例剖析
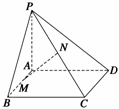
例1 如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
(1)求证:MN⊥CD; (2)若∠PDA=45°求证:MN⊥平面PCD.
证明 (1)连接AC,AN,BN,∵PA⊥平面ABCD,∴PA⊥AC,
在Rt△PAC中,N为PC中点, ∴AN=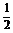 PC.
PC.
∵PA⊥平面ABCD, ∴PA⊥BC,又BC⊥AB,PA∩AB=A, ∴BC⊥平面PAB,∴BC⊥PB,
从而在Rt△PBC中,BN为斜边PC上的中线, ∴BN=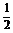 PC.∴AN=BN, ∴△ABN为等腰三角形,
PC.∴AN=BN, ∴△ABN为等腰三角形,
又M为底边的中点,∴MN⊥AB, 又∵AB∥CD,∴MN⊥CD.
(2)连接PM、CM,∵∠PDA=45°,PA⊥AD,∴AP=AD. ∵四边形ABCD为矩形.
∴AD=BC,∴PA=BC. 又∵M为AB的中点,∴AM=BM.
而∠PAM=∠CBM=90°,∴PM=CM. 又N为PC的中点,∴MN⊥PC. 由(1)知,MN⊥CD,PC∩CD=C,
∴MN⊥平面PCD.
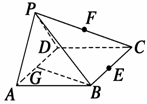 例2 如图所示,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD,若G为AD边的中点,(1)求证:BG⊥平面PAD; (2)求证:AD⊥PB;(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
例2 如图所示,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD,若G为AD边的中点,(1)求证:BG⊥平面PAD; (2)求证:AD⊥PB;(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
(1)证明 在菱形ABCD中,∠DAB=60°,G为AD的中点,所以BG⊥AD,
又平面PAD⊥平面ABCD, 平面PAD∩平面ABCD=AD, 所以BG⊥平面PAD.
(2)证明 连接PG,因为△PAD为正三角形, G为AD的中点,得PG⊥AD,
由(1)知BG⊥AD, PG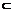 平面PGB,BG
平面PGB,BG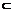 平面PGB,PG∩BG=G,
平面PGB,PG∩BG=G,
所以AD⊥平面PGB,因为PB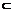 平面PGB, 所以AD⊥PB.
平面PGB, 所以AD⊥PB.
(3)解 当F为PC的中点时, 满足平面DEF⊥平面ABCD.证明如下: 取PC的中点F,连接DE、EF、DF,
在△PBC中,FE∥PB,在菱形ABCD中,
GB∥DE,而FE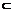 平面DEF,DE
平面DEF,DE 平面DEF,EF∩DE=E,所以平面DEF∥平面PGB,
平面DEF,EF∩DE=E,所以平面DEF∥平面PGB,
因为BG⊥平面PAD,所以BG⊥PG 又因为PG⊥AD,AD∩BG=G,
∴PG⊥平面ABCD,而PG 平面PGB,所以平面PGB⊥平面ABCD, 所以平面DEF⊥平面ABCD.
平面PGB,所以平面PGB⊥平面ABCD, 所以平面DEF⊥平面ABCD.
例3如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
(1)CD⊥AE;(2)PD⊥平面ABE.
 证明 (1)在四棱锥P-ABCD中, ∵PA⊥底面ABCD,CD
证明 (1)在四棱锥P-ABCD中, ∵PA⊥底面ABCD,CD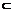 平面ABCD,∴PA⊥CD.
平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC. 而AE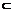 平面PAC,∴CD⊥AE.
平面PAC,∴CD⊥AE.
(2)由PA=AB=BC,∠ABC=60°,可得AC=PA. ∵E是PC的中点,∴AE⊥PC.
由(1)知,AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.而PD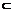 平面PCD,∴AE⊥PD.
平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,∴PA⊥AB. 又∵AB⊥AD且PA∩AD=A,
∴AB⊥平面PAD,而PD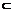 平面PAD,∴AB⊥PD. 又∵AB∩AE=A,综上得PD⊥平面ABE.
平面PAD,∴AB⊥PD. 又∵AB∩AE=A,综上得PD⊥平面ABE.
例4 如图所示,直三棱柱ABC-A1B1C1中,B1C1=A1C1, AC1⊥A1B,M、N分别是A1B1、AB的中点.
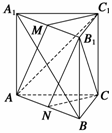 (1)求证:C1M⊥平面A1ABB1; (2)求证:A1B⊥AM;(3)求证:平面AMC1∥平面NB1C;(4)求A1B与B1C所成的角. (1)证明
方法一 由直棱柱性质可得AA1⊥平面A1B1C1,
(1)求证:C1M⊥平面A1ABB1; (2)求证:A1B⊥AM;(3)求证:平面AMC1∥平面NB1C;(4)求A1B与B1C所成的角. (1)证明
方法一 由直棱柱性质可得AA1⊥平面A1B1C1,
又∵C1M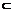 平面A1B1C1,∴AA1⊥MC1.又∵C1A1=C1B1,M为A1B1中点,∴C1M⊥A1B1.
平面A1B1C1,∴AA1⊥MC1.又∵C1A1=C1B1,M为A1B1中点,∴C1M⊥A1B1.
又A1B1∩A1A=A1, ∴C1M⊥平面AA1B1B.
(2)证明 由(1)知C1M⊥平面A1ABB1, ∴C1A在侧面AA1B1B上的射影为MA.
∵AC1⊥A1B,MC1⊥A1B,MC1∩AC1=C1, ∴A1B⊥平面AMC1,又AM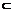 平面AMC1,
平面AMC1,
∴A1B⊥AM.
(3)证明 由(1)知C1M⊥平面AA1B1B, A1B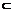 平面AA1B1B,∴C1M⊥A1B.
平面AA1B1B,∴C1M⊥A1B.
又∵A1B⊥AC1,而AC1∩C1M=C1, ∴A1B⊥平面AMC1. 同理可证,A1B⊥平面B1NC.
∴平面AMC1∥平面B1NC.
(4)解 方法一 由(2)知A1B⊥AM,又由已知A1B⊥AC1,AM∩AC1=A,∴A1B⊥平面AMC1.
又∵平面AMC1∥平面NB1C,∴A1B⊥平面NB1C. 又B1C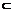 平面NB1C,∴A1B⊥B1C. ∴A1B与B1C所成的角为90°.
平面NB1C,∴A1B⊥B1C. ∴A1B与B1C所成的角为90°.
4.已知P为Rt△ABC所在平面外一点,且PA=PB=PC,D为斜边AB的中点,则直线PD与平面ABC. ( )
A.垂直 B.斜交 C.成600角 D.与两直角边长有关
3.直角△ABC的斜边BC在平面a内,顶点A在平面a外,则△ABC的两条直角边在平面a内的射影与斜边BC组成的图形只能是 ( )
A.一条线段 B.一个锐角三角形 C.一个钝角三角形 D.一条线段或一个钝角三角形
2.如果直线l⊥平面a,①若直线m⊥l,则m∥a; ②若m⊥a,则m∥l;③若m∥a,则m⊥l; ④若m∥l,则m⊥a,
上述判断正确的是 ( )
A.①②③ B.②③④ C.①③④ D.②④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com