
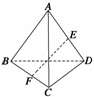
16.如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,
侧面PBC⊥底面ABCD.证明: (1)PA⊥BD; (2)平面PAD⊥平面PAB.
证明 (1)取BC的中点O, ∵平面PBC⊥平面ABCD,△PBC为等边三角形, ∴PO⊥底面ABCD.
以BC的中点O为坐标原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,如图所示,建立空间直角坐标系. 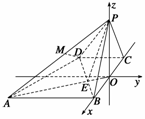 不妨设CD=1,则AB=BC=2,PO=
不妨设CD=1,则AB=BC=2,PO=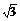 . ∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,
. ∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,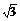 ).
).
∴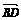 =(-2,-1,0),
=(-2,-1,0),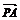 =(1,-2,-
=(1,-2,-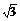 ).∵
).∵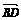 ·
·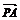 =(-2)×1+(-1)×(-2)+0×(-
=(-2)×1+(-1)×(-2)+0×(-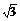 )=0,
)=0,
∴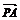 ⊥
⊥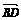 ,∴PA⊥BD.(2)取PA的中点M,连接DM,则M
,∴PA⊥BD.(2)取PA的中点M,连接DM,则M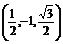 .
.
∵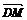 =
=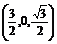 ,
,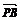 =(1,0,-
=(1,0,-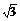 ),∴
),∴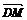 ·
·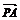 =
=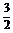 ×1+0×(-2)+
×1+0×(-2)+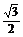 ×(-
×(-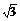 )=0,
)=0,
∴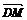 ⊥
⊥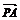 ,即DM⊥PA. 又
,即DM⊥PA. 又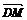 ·
·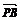 =
=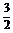 ×1+0×0+
×1+0×0+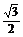 ×(-
×(-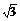 )=0,
)=0,
∴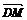 ⊥
⊥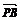 ,即DM⊥PB. 又∵PA∩PB=P,∴DM⊥平面PAB,
,即DM⊥PB. 又∵PA∩PB=P,∴DM⊥平面PAB,
∵DM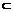 平面PAD.∴平面PAD⊥平面PAB.
平面PAD.∴平面PAD⊥平面PAB.
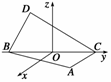
15.如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是 ,点D在平面yOz内,
,点D在平面yOz内,
且∠BDC=90°,∠DCB=30°. (1)求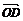 的坐标; (2)设
的坐标; (2)设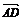 和
和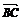 的夹角为
的夹角为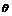 ,求cos
,求cos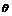 的值.
的值.
解 (1)如图所示,过D作DE⊥BC,垂足为E, 在Rt△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,
 得BD=1,CD=
得BD=1,CD=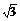 . ∴DE=CD·sin30°=
. ∴DE=CD·sin30°=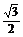 . OE=OB-BD·cos60°=1-
. OE=OB-BD·cos60°=1-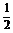 =
=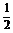 .
.
∴D点坐标为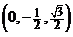 , 即
, 即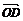 的坐标为
的坐标为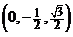 .
.
(2)依题意: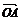 =
= , ?
, ? 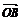 =(0,-1,0),
=(0,-1,0),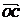 =(0,1,0). ∴
=(0,1,0). ∴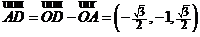 ,
,
? 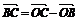 =(0,2,0). 设
=(0,2,0). 设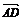 和
和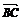 的夹角为
的夹角为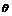 ,
,
则cos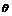 =
=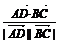
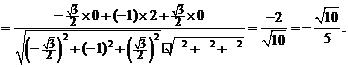 ∴cos
∴cos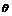 =--
=--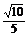 .
.
14.如图所示,正方体ABCD-A1B1C1D1,M为AA1的中点,N为A1B1上的点,且满足A1N=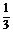 NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C.
NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C.
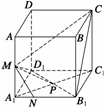 证明 设
证明 设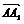 =a,
=a,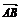 =b,
=b,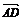 =c 则a、b、c两两垂直且模相等.∴a·b=b·c=a·c=0,
=c 则a、b、c两两垂直且模相等.∴a·b=b·c=a·c=0,
又∵A1N=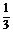 NB1 ∴
NB1 ∴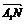 =
=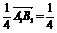 b,
b,
?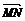 =
= +
+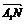 =
=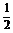 a+
a+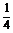 b, ?
b, ?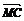 =
=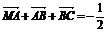 a+b+c,
a+b+c,
∴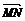 ·
·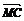 =
=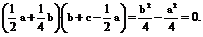
∴MN⊥MC,又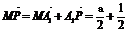 (b+c)=
(b+c)=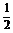 (a+b+c), ?
(a+b+c), ? 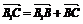 =-a+c.
=-a+c.
∴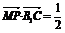 (a+b+c)(c-a)=0.∴MP⊥B1C.
(a+b+c)(c-a)=0.∴MP⊥B1C.
13.如图所示,已知空间四边形ABCD,F为BC的中点,E为AD的中点,
若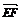 =
=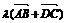 ,则
,则 =
0.5 .
=
0.5 .
12.若平面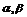 的法向量分别为n1=(2,3,5),n2=(-3,1,-4),则 (
C )
的法向量分别为n1=(2,3,5),n2=(-3,1,-4),则 (
C )
 ?A.
?A.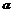 ∥
∥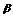 ? B.
? B. 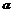 ⊥
⊥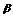 ?C.
?C. 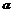 、
、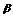 相交但不垂直 D.以上均不正确
相交但不垂直 D.以上均不正确
11.下列命题中不正确的命题个数是①若A、B、C、D是空间任意四点,则有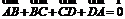 ②|a|-|b|=|a+b|是a、b共线的充要条件 ③若a、b共线,则a与b所在直线平行④对空间任意点O与不共线的三点A、B、C,若
②|a|-|b|=|a+b|是a、b共线的充要条件 ③若a、b共线,则a与b所在直线平行④对空间任意点O与不共线的三点A、B、C,若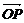 =x
=x +y
+y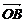 +z
+z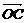 (其中x、y、z∈R),则P、A、B、C四点共面 ( C )
(其中x、y、z∈R),则P、A、B、C四点共面 ( C )
A.1 B.2 C.3 D.4
10.(2009·西安模拟)已知a=(1,1,1),b=(0,2,-1),c=ma+nb+(4,-4,1).若c与a及b都垂直,则m,n的值分别为( A )
?A.-1,2? B.1,-2? C.1,2 D.-1,-2
9.向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),下列结论正确的是 ( C )
A.a∥b,b⊥c? B.a∥b,a⊥c?C.a∥c,a⊥b? D.以上都不对
8.已知直线l的方向向量为v,平面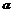 的法向量为u,则v·u=0,l与
的法向量为u,则v·u=0,l与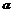 的关系是 (
D )
的关系是 (
D )
?A.l⊥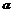 ? B.l∥
? B.l∥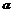 ? C.l
? C.l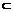
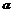 ? D.l∥
? D.l∥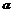 或l
或l
7.设平面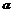 的法向量为(1,2,-2),平面
的法向量为(1,2,-2),平面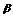 的法向量为(-2,-4,k),若
的法向量为(-2,-4,k),若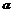 ∥
∥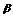 ,则k等于 (
C ) ?A.2? B.-4? C.4? D.-2
,则k等于 (
C ) ?A.2? B.-4? C.4? D.-2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com