
9.向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),下列结论正确的是 ( )
A.a∥b,b⊥c? B.a∥b,a⊥c?C.a∥c,a⊥b? D.以上都不对
8.已知直线l的方向向量为v,平面 的法向量为u,则v·u=0,l与
的法向量为u,则v·u=0,l与 的关系是 (
)
的关系是 (
)
?A.l⊥ ? B.l∥
? B.l∥ ? C.l
? C.l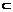
 ? D.l∥
? D.l∥ 或l
或l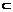

7.设平面 的法向量为(1,2,-2),平面
的法向量为(1,2,-2),平面 的法向量为(-2,-4,k),若
的法向量为(-2,-4,k),若 ∥
∥ ,则k等于 ( ) ?A.2? B.-4? C.4? D.-2
,则k等于 ( ) ?A.2? B.-4? C.4? D.-2
6.A、B、C、D是空间不共面的四点,且满足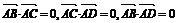 ,则△BCD是 ( )
,则△BCD是 ( )
?A.钝角三角形 B.锐角三角形 ?C.直角三角形 D.不确定
5.已知A(4,1,3),B(2,-5,1),C为线段AB上一点,且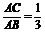 ,则C点的坐标为( ) A.
,则C点的坐标为( ) A.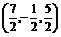 ? B.
? B.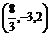 ?C.
?C.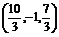 D.
D.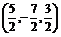
4.已知空间四边形ABCD的每条边和对角线的长都等于a,点E、F分别是BC、AD的中点,则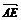 ·
·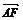 的值为( )
的值为( )
?A.a2? B.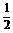 a2? C.
a2? C.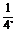 a2 ? D.
a2 ? D. a2
a2
3.(2009·东莞模拟)已知向量a,b满足|a|=2,|b|=3,|2a+b|=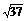 ,则a与b的夹角为 ( ) A.30° B.45°? C.60° D.90°?
,则a与b的夹角为 ( ) A.30° B.45°? C.60° D.90°?
2.已知向量a=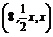 ,b=(x,1,2),其中x>0.若a∥b,则x的值为 ( ) A.8? B.4 ? C.2? D.0
,b=(x,1,2),其中x>0.若a∥b,则x的值为 ( ) A.8? B.4 ? C.2? D.0
1.已知点O、A、B、C为空间不共面的四点,且向量a=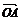 +
+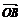 +
+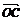 ,向量b=
,向量b=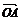 +
+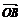 -
-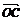 ,则与a,b不能构成空间基底的向量是 ( )
,则与a,b不能构成空间基底的向量是 ( )
A.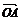 ? B.
? B.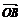 ? C.
? C.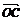 ? D.
? D.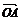 或
或
17.已知在直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.求证:
(1)BC1⊥AB1;(2)BC1∥平面CA1D.
证明 如图所示,以C1为原点,C1A1,C1B1,C1C所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
不妨设AC=2,由于AC=BC=BB1,则A(2,0,2),B(0,2,2),C(0,0,2),A1(2,0,0),B1(0,2,0),
 C1(0,0,0),D(1,1,2).
C1(0,0,0),D(1,1,2).
(1)由于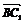 =(0,-2,-2), ?
=(0,-2,-2), ?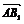 =(-2,2,-2),
=(-2,2,-2),
所以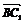 ·
·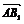 =0-4+4=0,因此
=0-4+4=0,因此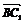 ⊥
⊥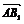 , 故BC1⊥AB1.
, 故BC1⊥AB1.
(2)方法一 取A1C的中点E,连接DE,由于E(1,0,1),
所以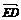 =(0,1,1),又
=(0,1,1),又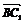 =(0,-2,-2),所以
=(0,-2,-2),所以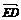 =-
=-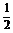 ·
·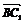 ,又因为ED和BC1不共线,
,又因为ED和BC1不共线,
所以ED∥BC1,且DE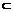 平面CA1D,BC1
平面CA1D,BC1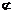 平面CA1D, 故BC1∥平面CA1D.
平面CA1D, 故BC1∥平面CA1D.
方法二 由于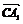 =(2,0,-2),
=(2,0,-2),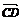 =(1,1,0), 若设
=(1,1,0), 若设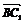 =x
=x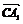 +y
+y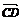 , 则得
, 则得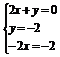 ,解得
,解得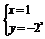
即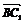 =
=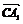 -2
-2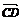 , 所以
, 所以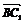 ,
,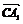 ,
,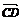 是共面向量,又因为BC1
是共面向量,又因为BC1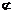 平面CA1D,因此BC1∥平面CA1D.
平面CA1D,因此BC1∥平面CA1D.
方法三 求出平面CA1D的法向量n,证明向量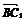 ⊥n. 设n=(a,b,1),由于
⊥n. 设n=(a,b,1),由于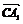 =(2,0,-2),
=(2,0,-2),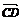 =(1,1,0) ∴
=(1,1,0) ∴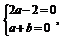 ,∴
,∴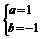 ∴n=(1,-1,1),又∵
∴n=(1,-1,1),又∵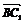 =(0,-2,-2),
=(0,-2,-2),
∴n·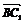 =2-2=0,∴
=2-2=0,∴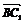 ⊥n,
⊥n,
又∵BC1 平面CA1D,∴BC1∥平面CA
平面CA1D,∴BC1∥平面CA
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com