
1.正方体ABCD-A1B1C1D1中,E、F分别是棱C1C与BC的中点,则直线EF与直线D1C所成角的大小是 ( B)
?A.45°? B.60°? C.75°? D.90°?
4.二面角:①定义:平面内的一条直线把平面分为两部分,其中的每一部分叫做半平面.从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面.二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角,叫做这个二面角的平面角.规定:二面角的两个半平面重合时,二面角为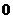 ,当两个半平面合成一个平面时,二面角为
,当两个半平面合成一个平面时,二面角为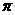 ,因此,二面角的大小范围为
,因此,二面角的大小范围为 .②确定二面角的方法:(1)定义法;(2)三垂线定理及其逆定理法;(3)垂面法;(4)射影面积法:
.②确定二面角的方法:(1)定义法;(2)三垂线定理及其逆定理法;(3)垂面法;(4)射影面积法: ,此方法常用于无棱二面角大小的计算;无棱二面角也可以先根据线面性质恢复二面角的棱,然后再用方法(1)、(2)计算大小;(5)向量法:法一、在
,此方法常用于无棱二面角大小的计算;无棱二面角也可以先根据线面性质恢复二面角的棱,然后再用方法(1)、(2)计算大小;(5)向量法:法一、在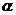 内
内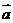
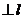 ,在
,在 内
内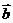
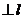 ,则二面角
,则二面角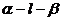 的平面角
的平面角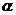
 ;或
;或  (同等异补)
(同等异补)
法二、设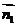 ,
, 是二面角
是二面角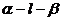 的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧(同等异补),则二面角
的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧(同等异补),则二面角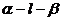 的平面角
的平面角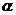

课前练习
2.异面直线所成角:(1)范围: ;(2)计算方法:①平移法:②向量法:设
;(2)计算方法:①平移法:②向量法:设 分别为异面直线
分别为异面直线 的方向向量,则两异面直线所成的角
的方向向量,则两异面直线所成的角
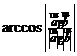 ;③补形法;④证明两条异面直线垂直,即所成角为
;③补形法;④证明两条异面直线垂直,即所成角为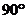 .
.
3直线与平面所成的角:①定义:平面的一条斜线和它在这个平面内的射影所成的锐角,若垂直于平面,所成角是直角.②范围
 ;③最小角定理:斜线和平面所成的角,是斜线和这个平面内经过斜足的直线所成的角中最小的角.⑤斜线与平面所成角的计算:(1)直接法:关键是作垂线,找射影
;③最小角定理:斜线和平面所成的角,是斜线和这个平面内经过斜足的直线所成的角中最小的角.⑤斜线与平面所成角的计算:(1)直接法:关键是作垂线,找射影 可利用面面垂直的性质;(2)通过等体积法求出斜线任一点到平面的距离
可利用面面垂直的性质;(2)通过等体积法求出斜线任一点到平面的距离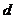 ,计算这点与斜足之间的线段长
,计算这点与斜足之间的线段长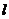 ,则
,则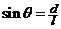 .(3)
.(3)  .
.
(4)向量法:设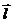 是斜线
是斜线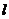 的方向向量,
的方向向量, 是平面
是平面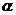 的法向量,则斜线
的法向量,则斜线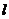 与平面
与平面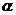 所成的角
所成的角
 .
.
1.空间角的计算步骤 一作、二证、三算.
一作、二证、三算.
3.AB⊥平面BCD,DC⊥CB,AD与平面BCD所成的角为30°,且AB=BC.
求AD与平面ABC所成角的大小.
 例1如图所示,过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=a,求: (1)二面角B-PC-D的大小; (2)平面PAB和平面PCD所成二面角的大小.
例1如图所示,过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=a,求: (1)二面角B-PC-D的大小; (2)平面PAB和平面PCD所成二面角的大小.
例2(2008·重庆理,19)如图所示,在△ABC中,B=90°,AC=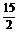 ,D、E两点分别在AB、AC上,使
,D、E两点分别在AB、AC上,使 =2,
=2,
 DE=3.现将△ABC沿DE折成直二面角.求: (1)异面直线AD与BC的距离;(2)二面角A-EC-B的大小。
DE=3.现将△ABC沿DE折成直二面角.求: (1)异面直线AD与BC的距离;(2)二面角A-EC-B的大小。
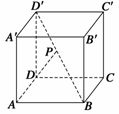
例3(2008·海南理,18)如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小; (2)求DP与平面AA′D′D所成角的大小.
例4如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8.BC是⊙O
 的直径,AB=AC=6,OE∥AD. (1)求二面角B-AD-F的大小; (2)求直线BD与EF所成的角的余弦值.
的直径,AB=AC=6,OE∥AD. (1)求二面角B-AD-F的大小; (2)求直线BD与EF所成的角的余弦值.
2.一副三角板如图拼接,使两个三角板所在的平面互相垂直.如果公共边AC=a,则异面直线AB与CD的距离是( )?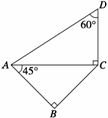 A.
A. B.a? C.
B.a? C.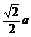 ? D.
? D.
1.正方体ABCD-A1B1C1D1中,E、F分别是棱C1C与BC的中点,则直线EF与直线D1C所成角的大小是 ( )
?A.45°? B.60°? C.75°? D.90°?
4.二面角:①定义:
.②确定二面角的方法:(1)定义法;(2)
;(3)
;(4)射影面积法: ,( 5)向量法:法一、在
,( 5)向量法:法一、在 内
内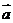
 ,在
,在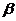 内
内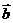
 ,则二面角
,则二面角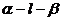 的平面角
的平面角 ;或
;或
法二、设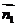 ,
, 是二面角
是二面角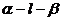 的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧(同等异补),则二面角
的两个半平面的法向量,其方向一个指向内侧,另一个指向外侧(同等异补),则二面角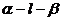 的平面角
的平面角
课前练习
2.异面直线所成角:(1)范围:
;(2)计算方法:①平移法:②向量法:设 分别为异面直线
分别为异面直线 的方向向量,则两异面直线所成的角
的方向向量,则两异面直线所成的角 ;③补形法;④证明两条异面直线垂直,即所成角为
;③补形法;④证明两条异面直线垂直,即所成角为 .
.
3直线与平面所成的角:①定义:
若垂直于平面,所成角
.②范围 ;③最小角定理:斜线和平面所成的角,是斜线
直线所成的角中最小的角.⑤斜线与平面所成角的计算:(1)直接法:关键是 ,找射影
;③最小角定理:斜线和平面所成的角,是斜线
直线所成的角中最小的角.⑤斜线与平面所成角的计算:(1)直接法:关键是 ,找射影 (2)通过等体积法求出斜线任一点到平面的 ,计算这点与斜足之间的线段长
(2)通过等体积法求出斜线任一点到平面的 ,计算这点与斜足之间的线段长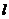 ,则
,则 .(3) 公式:
.
.(3) 公式:
.
(4)向量法:设 是斜线
是斜线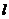 的方向向量,
的方向向量, 是平面
是平面 的法向量,则斜线
的法向量,则斜线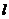 与平面
与平面 所成的角
所成的角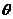 =
.
=
.
1.空间角的计算步骤 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com