
8.正方体ABCD-A1B1C1D1的棱长为a,E是CC1的中点,则E到A1B的距离是 (D )
A. 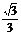 a B.
a B. 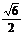 a C.
a C. 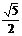 a D.
a D. 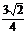 a
a
7. 一个山坡面与水平面成1200的二面角,坡脚的水平线为AB,甲沿山坡自P朝垂直于AB的方向走30m,同时乙沿水平面自Q朝垂直于AB的方向走30m,P、Q都是AB上的点,若PQ=10m,这时甲、乙2个人之间的距离为 ( B )
A.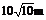 B.
B.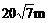 C.
C.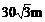 D.
D.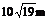
6.△ABC中,AB=9,AC=15,∠BAC=120°.△ABC所在平面外一点P到三个顶点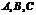 的距离都是14,那么点P到
的距离都是14,那么点P到
平面ABC的距离为 (A )
?A.7? B.9? C.11 D.13
5.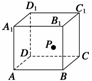 .如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与
.如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与
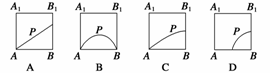
直线BC的距离相等, 则动点P所在的曲线形状为 ( C )
4..已知平面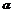 ∥平面
∥平面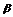 ,直线l
,直线l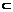
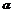 ,点P∈l,平面
,点P∈l,平面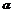 、
、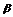 间的距离为a,则在
间的距离为a,则在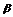 内到点P的距离为c,且到直线l的距离为b (a<b<c)的点的轨迹 ( D? )
内到点P的距离为c,且到直线l的距离为b (a<b<c)的点的轨迹 ( D? )
?A.是一个圆? B.是两条直线 ?C.不存在? D.是四个点
3.正方体ABCD-A1B1C1D1的棱长为1,E、F分别为BB1、CD的中点,则点F到平面A1D1E的距离为( C )
?A.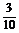 B.
B.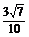 ? C.
? C.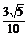 ?D.
?D.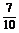
2.正方体ABCD-A1B1C1D1的棱长为1,O是A1C1的中点,则点O到平面ABC1D1的距离为( B )
A.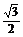 ? B.
? B.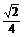 ? C.
? C.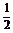 D.
D.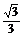
1.如图所示,在空间直角坐标系中,有一棱长为a的正方
体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为(B )
?A.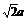 ? B.
? B.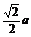 ? C.a? D.
? C.a? D.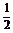 a
a
3.AB⊥平面BCD,DC⊥CB,AD与平面BCD所成的角为30°,且AB=BC.
求AD与平面ABC所成角的大小.( 45°)
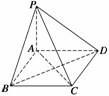 例1如图所示,过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=a,求: (1)二面角B-PC-D的大小; (2)平面PAB和平面PCD所成二面角的大小.
例1如图所示,过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=a,求: (1)二面角B-PC-D的大小; (2)平面PAB和平面PCD所成二面角的大小.
解 (1)∵PA⊥平面ABCD,BD⊥AC,∴BD⊥PC(三垂线定理)
在平面PBC内,作BE⊥PC,E为垂足,连结DE,得PC⊥平面BED,
从而DE⊥PC,即∠BED是二面角B-PC-D的平面角.
在Rt△PAB中,由PA=AB=a,得PB=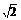 a. ∵PA⊥平面ABCD,BC⊥AB,
a. ∵PA⊥平面ABCD,BC⊥AB,
∴BC⊥PB(三垂线定理) ∴PC=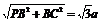
在Rt△PBC中,BE=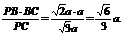 同理DE=
同理DE=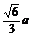 .
.
 在△BDE中,根据余弦定理,得 ?cos∠BED=
在△BDE中,根据余弦定理,得 ?cos∠BED=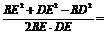
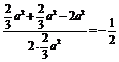 .
.
∴∠BED=120°,即二面角B-PC-D的大小为120°.
(2)过P作PQ∥AB,则PQ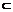 平面PAB. ∵AB∥CD,∴PQ∥CD,PQ
平面PAB. ∵AB∥CD,∴PQ∥CD,PQ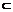 平面PCD.
平面PCD.
∵PA⊥AB,∴PA⊥PQ ∵PA⊥平面ABCD,CD⊥AD.
∴CD⊥PD即QP⊥PD, 则∠APD即为所求的二面角,
∵PA=AD=a,PA⊥AD, ∴∠APD=45°? 即所求的二面角的大小为45°.
例2(2008·重庆理,19)如图所示,在△ABC中,B=90°,AC=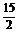 ,D、E两点分别在AB、AC上,使
,D、E两点分别在AB、AC上,使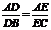 =2,
=2,
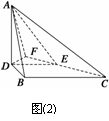
DE=3.现将△ABC沿DE折成直二面角.求: (1)异面直线AD与BC的距离;(2)二面角A-EC-B的大小。
解 方法一 (1)在图(1)中,因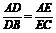 , 故DE∥BC. 又因为B=90°,从而AD⊥DE. 在图(2)中,因二面角A-DE-B是直二面角,AD⊥DE,故AD⊥底面DBCE,从而AD⊥DB.而DB⊥BC,故DB为异面直线AD与BC的公垂线. 下面求DB的长,在图(1)中,
, 故DE∥BC. 又因为B=90°,从而AD⊥DE. 在图(2)中,因二面角A-DE-B是直二面角,AD⊥DE,故AD⊥底面DBCE,从而AD⊥DB.而DB⊥BC,故DB为异面直线AD与BC的公垂线. 下面求DB的长,在图(1)中,
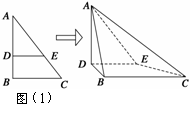 由
由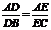 =2,得
=2,得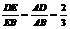 .
.
又已知DE=3,从而BC=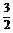 DE=
DE=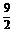 .
.
AB=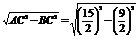 =6.
=6.
因为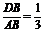 ,所以DB=2. 故异面直线AD与BC的距离为2.
(2)在图(2)中,过D作DF⊥CE,交CE的延长线于点F,连接AF,由(1)知,AD⊥底面DBCE.由三垂线定理知AF⊥FC, 故∠AFD为二面角A-EC-B的平面角.在底面DBCF中,∠DEF=∠BCE, DB=2,EC=
,所以DB=2. 故异面直线AD与BC的距离为2.
(2)在图(2)中,过D作DF⊥CE,交CE的延长线于点F,连接AF,由(1)知,AD⊥底面DBCE.由三垂线定理知AF⊥FC, 故∠AFD为二面角A-EC-B的平面角.在底面DBCF中,∠DEF=∠BCE, DB=2,EC=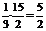 ,
,
因此sin∠BCE=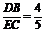 ,从而在Rt△DFE中,DE=3,
,从而在Rt△DFE中,DE=3,
DF=DEsin∠DEF=DEsin∠BCE=3·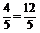 . 在Rt△AFD中,AD=4,tan∠AFD=
. 在Rt△AFD中,AD=4,tan∠AFD=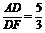 .
.
因此所求二面角A-EC-B的大小为arctan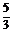 .
.
方法二 (1)同方法一.
(2)由(1)可知,以D点为坐标原点, 的方向为x、y、z轴的正方向建立空间直角坐标系,
的方向为x、y、z轴的正方向建立空间直角坐标系,
如图(3),则D(0,0,0),A(0,0,4),C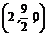 ,E(0,3,0),
,E(0,3,0),
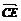 =(-2,-
=(-2,-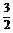 ,0),
,0),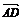 =(0,0,-4),过D作DF⊥CE,交CE的延长线于点F,连接AF.
=(0,0,-4),过D作DF⊥CE,交CE的延长线于点F,连接AF.
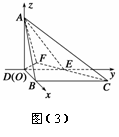 设F(x0,y0,0),从而
设F(x0,y0,0),从而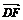 =(x0,y0,0).
=(x0,y0,0). 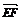 =(x0,y0-3,0).由DF⊥CE,得 ?
=(x0,y0-3,0).由DF⊥CE,得 ? 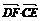 =0,即2x0+
=0,即2x0+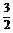 y0=0. ①
y0=0. ①
又由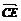 ∥
∥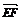 ,得
,得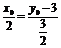 . ②
. ②
联立①,②,解得x0=-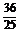 ,y0=
,y0=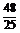 , 即F
, 即F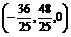 ,得
,得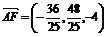 .
.
因为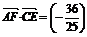 ·(-2)+
·(-2)+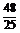 ·
·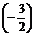 =0,
=0,
故AF⊥CE.又因为DF⊥CE, 所以∠DFA为所求的二面角A-EC-B的平面角.因为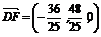 ,
,
所以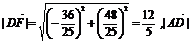 =4, 所以tan∠AFD=
=4, 所以tan∠AFD=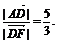
因此所求二面角A-EC-B的大小为arctan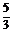 .
.
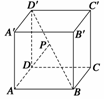
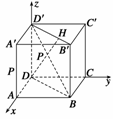
例3(2008·海南理,18)如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小; (2)求DP与平面AA′D′D所成角的大小.
解 如图所示,以D为原点,DA为单位长度建立空间直角坐标系D-xyz.
则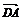 =(1,0,0),
=(1,0,0),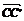 =(0,0,1).连接BD,B′D′.在平面BB′D′D中, 延长DP交B′D′于H.
=(0,0,1).连接BD,B′D′.在平面BB′D′D中, 延长DP交B′D′于H.
 设
设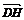 =(m,m,1)(m>0),由已知〈
=(m,m,1)(m>0),由已知〈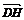 ,
,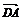 〉=60°,
〉=60°,
由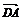 ·
·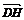 =|
=|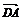 ||
||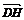 |cos〈
|cos〈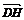 ,
,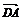 〉,可得2m=
〉,可得2m=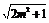 .
.
解得m=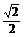 ,所以
,所以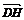 =
=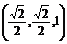 .
.
 (1)因为cos〈
(1)因为cos〈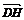 ,
,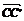 〉=
〉=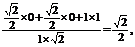 所以〈
所以〈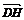 ,
,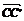 〉=45°,
〉=45°,
即DP与CC′所成的角为45°.
(2)平面AA′D′D的一个法向量是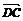 =(0,1,0).
=(0,1,0).
因为cos〈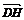 ,
,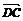 〉=
〉=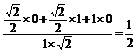 ,
,
所以〈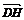 ,
,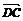 〉=60°, 可得DP与平面AA′D′D所成的角为30°.
〉=60°, 可得DP与平面AA′D′D所成的角为30°.
例4如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8.BC是⊙O
的直径,AB=AC=6,OE∥AD.
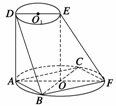 (1)求二面角B-AD-F的大小;
(1)求二面角B-AD-F的大小;
(2)求直线BD与EF所成的角的余弦值.
解 (1)∵AD与两圆所在的平面均垂直,
∴AD⊥AB,AD⊥AF,
故∠BAF是二面角B-AD-F的平面角.
依题意可知,四边形ABFC是正方形,
∴∠BAF=45°.
即二面角B-AD-F的大小为45°;
(2)以O为原点,CB、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),
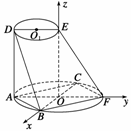 则O(0,0,0),A(0,-3
则O(0,0,0),A(0,-3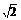 ,0),
,0),
B(3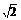 ,0,0),D(0,-3
,0,0),D(0,-3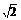 ,8),
,8),
E(0,0,8),F(0,3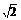 ,0),
,0),
∴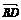 =(-3
=(-3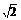 ,-3
,-3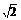 ,8),
,8),
?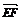 =(0,3
=(0,3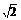 ,-8).
,-8).
?cos〈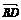 ,
,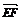 〉=
〉=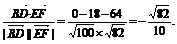
设异面直线BD与EF所成角为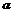 ,则
,则
?cos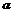 =|cos〈
=|cos〈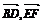 〉|=
〉|= .
.
即直线BD与EF所成的角的余弦值为 .
.
2.一副三角板如图拼接,使两个三角板所在的平面互相垂直.如果公共边AC=a,则异面直线AB与CD的距离是(C )?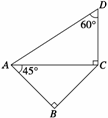 A.
A.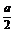 B.a? C.
B.a? C.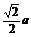 ? D.
? D.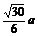
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com