
1.在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为( ) ?A.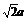 ? B.
? B. ? C.a? D.
? C.a? D.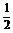 a
a
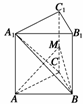
12.如图所示,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=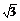 ,AA1=
,AA1=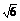 ,M是侧棱CC1的中点.
,M是侧棱CC1的中点.
(1)求证:AM⊥BA1; (2)求证:平面ABM⊥平面A1BC; (3)求点C到平面ABM的距离.
(1)证明 在Rt△A1AC与Rt△ACM中,
 ∵
∵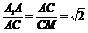 ,∴ Rt△A1AC∽Rt△ACM. ∴∠AA1C=∠CAM.
,∴ Rt△A1AC∽Rt△ACM. ∴∠AA1C=∠CAM.
∴∠AA1C=∠CAM.∴A1C⊥AM. ∵BC⊥AC,BC⊥CC1,且AC∩CC1=C,
∴BC⊥平面CC1A1A,A1C是BA1在平面CC1A1A内的射影.
又AM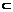 平面CC1A1A,∴BA1⊥AM.
平面CC1A1A,∴BA1⊥AM.
(2)证明 由(1)知AM⊥BA1,AM⊥A1C, 且BA1∩A1C=A1,
∴AM⊥平面A1BC.又AM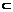 平面ABM, ∴平面ABM⊥平面A1BC.
平面ABM, ∴平面ABM⊥平面A1BC.
(3)解 设点C到平面ABM的距离为h. 由VM-ABC=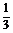 S△ABC·MC =
S△ABC·MC =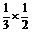 BC·AC·MC=
BC·AC·MC=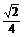 ,
,
易知AM=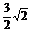 ,BM=
,BM=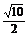 ,AB=2, ∴cos∠AMB=
,AB=2, ∴cos∠AMB=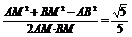 .
.
∴sin∠AMB=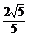 . ∴S△ABM=
. ∴S△ABM=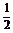 ·AM·BM·sin∠AMB=
·AM·BM·sin∠AMB=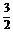 . ∵VC-ABM=VM-ABC,
. ∵VC-ABM=VM-ABC,
故h= ,即点C到平面ABM的距离为
,即点C到平面ABM的距离为 .
.
11.已知正三棱柱ABC-A1B1C1的底面边长为8,对角线B1C=10,D是AC的中点.
(1)求点B1到直线AC的距离; (2)求直线AB1到面C1BD的距离.
解 (1)连结BD、B1D, ∵由三垂线定理可知B1D⊥AC,
∴B1D就是点B1到直线AC的距离. 在Rt△B1BD中,
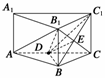 ∴BB1=
∴BB1=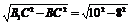 =6,BD=4
=6,BD=4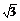 , ∴B1D=
, ∴B1D=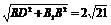 ,
,
即点B1到直线AC的距离为2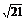 .
.
(2)设B1C与BC1交于点E,连结DE 则DE∥AB1,又∵AB1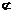 平面C1BD,
平面C1BD,
∴AB1∥平面C1BD. 又AC与面BDC1交于AC的中点D,
∴AB1到平面BDC1的距离等于A点到面BDC1的距离,也就等于三棱锥C-BDC1的高.
∵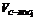 =
=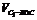 , ∴
, ∴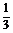 ×h×S△BDC1=
×h×S△BDC1=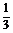 ×S△BDC×CC1. ∴h=
×S△BDC×CC1. ∴h=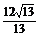 ,
,
∴直线AB1到平面BDC1的距离是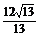 .
.
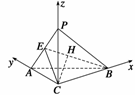
10.如图所示,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
(1)求证:PC⊥AB; (2)求二面角B-AP-C的大小; (3)求点C到平面APB的距离.
方法一 (1)证明 如,取AB中点D,连结PD,CD.
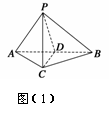 ∵AP=BP,∴PD⊥AB. ∵AC=BC,∴CD⊥AB. 图(1)
∵AP=BP,∴PD⊥AB. ∵AC=BC,∴CD⊥AB. 图(1)
∵PD∩CD=D,∴AB⊥平面PCD. ∵PC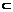 平面PCD,∴PC⊥AB.
平面PCD,∴PC⊥AB.
(2)解 ∵AC=BC,AP=BP,PC=PC,
∴△APC≌△BPC. 又PC⊥AC,∴PC⊥BC.
又∠ACB=90°,即AC⊥BC, 且AC∩PC=C,∴BC⊥平面PAC.
如图(2),取AP中点E,连结BE,CE. ∵AB=BP,∴BE⊥AP.
 ∵EC是BE在平面PAC内的射影,∴CE⊥AP.
∵EC是BE在平面PAC内的射影,∴CE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
在△BCE中,∠BCE=90°,BC=2,BE=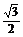 AB=
AB=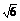 ,
,
∴sin∠BEC=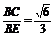 . ∴二面角B-AP-C的大小为arcsin
. ∴二面角B-AP-C的大小为arcsin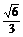 .
.
(3)解 由(1)知AB⊥平面PCD, ∴平面APB⊥平面PCD. 如图(3),过C作CH⊥PD,垂足为H.
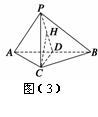 ∵平面APB∩平面PCD=PD, ∴CH⊥平面APB.
∵平面APB∩平面PCD=PD, ∴CH⊥平面APB.
∴CH的长即为点C到平面APB的距离.
由(1)知PC⊥AB,又PC⊥AC, 且AB∩AC=A,∴PC⊥平面ABC.
∵CD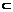 平面ABC,∴PC⊥CD.
平面ABC,∴PC⊥CD.
在Rt△PCD中,CD=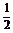 AB=
AB=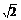 ,PD=
,PD=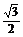 PB=
PB=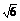 , ∴PC=
, ∴PC=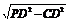 =2.
=2.
∴CH= . ∴点C到平面APB的距离为
. ∴点C到平面APB的距离为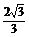 .
.
 方法二 (1)证明 ∵AC=BC,AP=BP,CP=CP, ∴△APC≌△BPC.
方法二 (1)证明 ∵AC=BC,AP=BP,CP=CP, ∴△APC≌△BPC.
又PC⊥AC,∴PC⊥BC. ∵AC∩BC=C,∴PC⊥平面ABC.
∵AB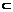 平面ABC,∴PC⊥AB.
平面ABC,∴PC⊥AB.
(2)解 如图所示,以C为原点建立空间直角坐标系C-xyz.
则C(0,0,0),A(0,2,0), B(2,0,0),设P(0,0,t).
∵|PB|=|AB|=2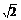 , ∴t=2,P(0,0,2).
, ∴t=2,P(0,0,2).
取AP中点E,连结BE,CE. ∵|AC|=|PC|,|AB|=|BP|, ∴CE⊥AP,BE⊥AP.
∴∠BEC是二面角B-AP-C的平面角. ∵E(0,1,1),∴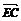 =(0,-1,-1),
=(0,-1,-1),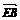 =(2,-1,-1),
=(2,-1,-1),
∴cos∠BEC=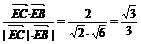 . ∴二面角B-AP-C的大小为arccos
. ∴二面角B-AP-C的大小为arccos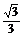 .
.
(3)解 ∵AC=BC=PC, ∴C在平面APB内的射影为正△APB的中心H,
且CH的长为点C到平面APB的距离. 如(2)建立空间直角坐标系C-xyz.
∵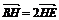 ,∴点H的坐标为
,∴点H的坐标为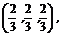 ∴
∴ , ∴点C到平面APB的距离为
, ∴点C到平面APB的距离为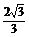 .
.
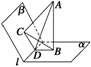
14.已知二面角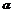 -l-
-l-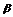 的大小为120°,A是它内部的一点,AB⊥
的大小为120°,A是它内部的一点,AB⊥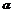 ,AC⊥
,AC⊥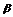 ,B、C为垂足,平面ABC交棱l于D点. (1)求证:平面ABC⊥
,B、C为垂足,平面ABC交棱l于D点. (1)求证:平面ABC⊥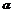 ,平面ABC⊥
,平面ABC⊥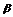 ; (2)若AB=4 cm?,AC=6 cm?,求BC的长及AD的长.
; (2)若AB=4 cm?,AC=6 cm?,求BC的长及AD的长.
 (1)证明 ∵AB⊥
(1)证明 ∵AB⊥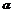 ,AC⊥
,AC⊥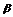 ,
,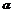 ∩
∩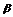 =l, ∴AB⊥l,AC⊥l,AB∩AC=A,
=l, ∴AB⊥l,AC⊥l,AB∩AC=A,
∴l⊥平面ABC, ∴平面ABC⊥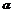 ,平面ABC⊥
,平面ABC⊥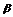 .
.
(2)解 ∵平面ABC交棱l于D点,连结CD、BD、AD,
则CD⊥l,BD⊥l,AD⊥l, ∴∠CDB=120°,∠CAB=60°?
△ABC中,BC=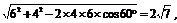 , 显然,A、B、C、D四点共圆,AD为直径,由正弦定理得AD=
, 显然,A、B、C、D四点共圆,AD为直径,由正弦定理得AD=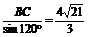 .
. 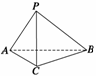 ∴BC的长为2
∴BC的长为2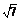 cm,AD的长为
cm,AD的长为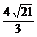 cm.
cm.
13.已知l1、l2是两条异面直线,α、β、γ是三个平面依次互相平行,l1、l2分别交α、β、γ于A、B、C和D、E、F,AB=4,BC=12,DF=10,又l1与α成30°角,则β与γ的距离是___6_______;DE=___ 2.5_______.
12.在正三棱柱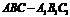 中,
中,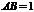 .若二面角
.若二面角 的大小为
的大小为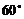 ,则点
,则点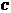 到平面
到平面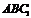 的距离为_
的距离为_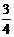 ____.
____.
11.正三棱锥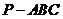 的高为
的高为 ,侧棱与底面
,侧棱与底面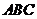 成
成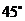 角,则点
角,则点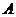 到侧面
到侧面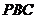 的距离为___
的距离为___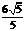 __.
__.
10.设PA⊥Rt△ABC所在的平面α,∠BAC=90°,PB、PC分别与α成45°和30°角,PA=2,则PA与BC的距离是___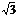 ______;点P到BC的距离是__
______;点P到BC的距离是__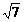 _____.
_____.
9.平面α内的∠MON=60°,PO是α的斜线,PO=3,∠POM=∠PON=45°,那么点P到平面α的距离 ( A )
A. 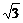 B.
B.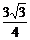 C.
C. 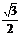 D.
D. 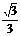
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com