
4.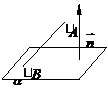 点到平面的距离:
点到平面的距离:
求法:(1)直接法:(2)等体积法:(3)转化为线面平行法:(4)线段比例转化法:(5)向量法:
设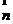 是平面
是平面 的法向量,在
的法向量,在 内取一点
内取一点 , 则
, 则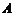 到
到 的距离
的距离
3.两条异面直线的距离:两条异面直线的公垂线段的长度.
求法:(1)直接法:求两异面直线的公垂线段的长度;(2)转化法:转化为线面距离或面面距离;
2.点与点的距离:(1)解三角形及多边形;(2)向量法:空间任意两点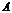 、
、 间的距离即线段
间的距离即线段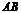 的长度:设
的长度:设 、
、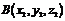 ,则
,则
1.七种距离:点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离,其中点与点、点与直线、点到平面的距离是基础,求其它几种距离一般化归为求这三种距离.
4.在Rt△ABC中,∠C=30°,∠B=90°,D是BC边的中点,AC=2,DE⊥平面ABC,DE=1,则点E到斜边AC的
距离是 ( )
A.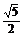 ? B.
? B.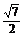 ? C.
? C. ? D.
? D.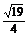
典例剖析:
 例1.如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=a,D、E分别为棱AB、BC的中点,M为棱AA1上的点,二面角M-DE-A为30°.
例1.如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=a,D、E分别为棱AB、BC的中点,M为棱AA1上的点,二面角M-DE-A为30°.
(1)证明:A1B1⊥C1D; (2)求MA的长,并求点C到平面MDE的距离.
例2.已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=1,E、F分别是AB、BC的中点.
(1)求D点到平面PEF的距离; (2)求直线AC到平面PEF的距离.

 例3.如图,在直三棱柱
例3.如图,在直三棱柱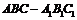 中,
中, ,
,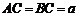 ,
, 分别为棱
分别为棱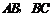 的中点,
的中点,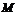 为棱
为棱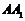 上的点,二面角
上的点,二面角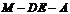 为
为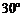 .(1)证明:
.(1)证明: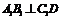 (此小题略去不写);(2)求
(此小题略去不写);(2)求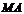 的长,并求点
的长,并求点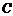 到平面
到平面 的距离. (请用多种方法,至少要用向量法)
的距离. (请用多种方法,至少要用向量法)
 例4.如图,在直三棱柱ABC-
例4.如图,在直三棱柱ABC-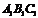 中,
中,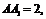 AB = 1,
AB = 1,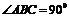 ;点D、E分别在
;点D、E分别在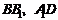 上,且
上,且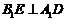 ,四棱锥
,四棱锥 与直三棱柱的体积之比为3:5。(1)求异面直线DE与
与直三棱柱的体积之比为3:5。(1)求异面直线DE与 的距离;(2)若BC =
的距离;(2)若BC =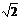 ,求二面角
,求二面角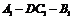 的平面角的正切值。
的平面角的正切值。
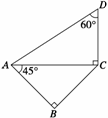
3.一副三角板如图拼接,使两个三角板所在的平面互相垂直.如果公共边AC=a,
则异面直线AB与CD的距离是( )?
A. B.a? C.
B.a? C.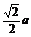 D.
D.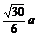
1.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离为 ( )
 ?A.
?A.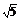 ? B.2
? B.2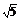 ? C.3
? C.3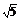 ? D.4
? D.4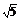
7.求距离的一般步骤:① ;②证明 ;③归到某三角形或多边形中计算;④作答.
课前练习:
6.距离的共性:这其中距离中,虽然定义不同,但总具有下列几个特征:
①指相应线段的长度;②相关线段中最短的;③除两点间距离外,其余总与垂直相联系,方法就有几何法和代数等方法.
5.直线到平面的距离:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com