
1.具有下列性质的三棱锥中,哪一个是正棱锥 ( )
?A.顶点在底面上的射影到底面各顶点的距离相等 ?B.底面是正三角形,且侧面都是等腰三角形
?C.相邻两条侧棱的夹角相等 ?D.三条侧棱相等,侧面与底面所成角也相等
19.三棱柱ABC-A′B′C′的所有棱长均为a,∠A′AB=∠A′AC=60°,求其全面积.
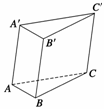 解 如图所示,过B作BD⊥AA′于D,连结CD,则△BAD≌△CAD.
解 如图所示,过B作BD⊥AA′于D,连结CD,则△BAD≌△CAD.
∴∠ADB=∠ADC=90°, ∴AD⊥CD,∴AD⊥BD.
∴△BCD为直截面.(垂直于侧棱的截面叫做直截面)
∵∠BAD=60°,AB=a,∴BD= .
.
 ∴△BDC的周长为(
∴△BDC的周长为(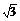 +1)a.
+1)a.
则S侧=(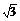 +1)a2,(侧面积=直截面的周长×侧棱长)
+1)a2,(侧面积=直截面的周长×侧棱长)
S底=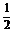 ·a·a·sin60°=
·a·a·sin60°=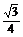 a2, ∴S全=S侧+2S底=
a2, ∴S全=S侧+2S底=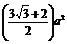
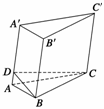
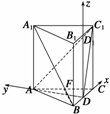
18.如图所示,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,AB= ,BB1=2,BC=1,∠BCC1=
,BB1=2,BC=1,∠BCC1=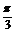 ,求:(1)异面直线AB与EB1的距离;(2)二面角A-EB1-A1的平面角的正切值.
,求:(1)异面直线AB与EB1的距离;(2)二面角A-EB1-A1的平面角的正切值.
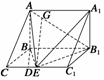 解 (1)AB⊥面BB1C1C,故AB⊥BE. 又BE1⊥EA,且EA在面BCC1B1内的射影为EB.
解 (1)AB⊥面BB1C1C,故AB⊥BE. 又BE1⊥EA,且EA在面BCC1B1内的射影为EB.
由三垂线定理的逆定理知EB1⊥BE. 因此BE是异面直线AB与EB1的公垂线.
在平行四边形BCC1B1中, 设EB=x,则EB1=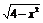 .
.
作BD⊥CC1,交CC1于D,则BD=BC·sin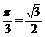 .在△BEB1中,由面积关系得
.在△BEB1中,由面积关系得
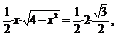 即(x22-1)(x2-3)=0.解之得x=±1,x=±
即(x22-1)(x2-3)=0.解之得x=±1,x=±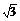 (负根舍去).
(负根舍去).
当x=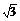 时,在△BCE中,CE2+12-2CE·cos
时,在△BCE中,CE2+12-2CE·cos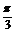 =3,解之得CE=2,
=3,解之得CE=2,
故此时E与C1重合,由题意舍去x=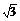 .因此x=1,即异面直线AB与EB1的距离为1.
.因此x=1,即异面直线AB与EB1的距离为1.
(2)过E作EG∥B1A1,则GE⊥面BCC1B1, 故GE⊥EB1,且GE在面A1B1E内.又已知AE⊥EB1,
故∠AEG是二面角A-EB1-A1的平面角. 因为EG∥B1A1∥BA,∠AEG=∠BAE,
故tan∠AEG=tan∠BAE=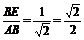 .
.
17.如图所示,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M为AA1中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短距离长为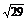 ,设这条最短路线与CC1的交点为N,求:(1)该三棱柱的侧面展开图的对角线长;
,设这条最短路线与CC1的交点为N,求:(1)该三棱柱的侧面展开图的对角线长;
(2)PC与NC的长; (3)此棱柱的表面积.
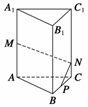 解(1)正三棱柱ABC-A1B1C1侧面展开图是一个长为9,宽为4的矩形,其对角线长为
解(1)正三棱柱ABC-A1B1C1侧面展开图是一个长为9,宽为4的矩形,其对角线长为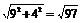 . (2)如图,将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上,点P运动到点P1的位置,连结MP1,则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线.
. (2)如图,将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上,点P运动到点P1的位置,连结MP1,则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线.
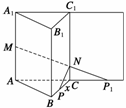 设PC=x,即P1C=x, 在Rt△MAP1中,由勾股定理得(3+x)2+22=29,
设PC=x,即P1C=x, 在Rt△MAP1中,由勾股定理得(3+x)2+22=29,
求得x=2,∴PC=P1C=2.
∵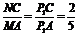 ,∴NC=
,∴NC=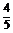 .
.
 (3)棱柱的表面积: S=S侧+2S底=9×4+2×
(3)棱柱的表面积: S=S侧+2S底=9×4+2×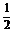 ×
×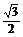 ×32=
×32=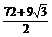 .
.
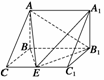
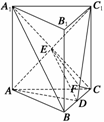
16.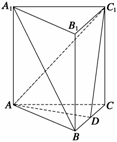 如图所示,在正三棱柱ABC-A1B1C1中,AB=AA1,D是BC的中点.
如图所示,在正三棱柱ABC-A1B1C1中,AB=AA1,D是BC的中点.
(1)求证:A1B∥平面AC1D; (2)求二面角C-AC1-D的大小.
(1)证明 ∵ABC-A1B1C1是正三棱柱,D是BC的中点. 连结AC1与A1C相交于E点,
在△A1BC中,∵D、E是中点, ∴A1B∥DE,又DE在平面AC1D内,∴A1B∥平面AC1D.
(2)解 方法一 作CF⊥C1D于F,则CF⊥平面AC1D,
连结EF,∵CE⊥AC1,∴EF⊥AC1, ∴∠CEF就是二面角C-AC1-D的平面角.
 令CD=1,则CC1=2,∴CF=
令CD=1,则CC1=2,∴CF=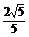 ,CE=
,CE= ,∴sin∠CEF=
,∴sin∠CEF=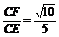 ,
,
即二面角C-AC1-D的大小为arcsin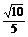 .
.
方法二 设D1是B1C1的中点,以DC所在直线为x轴,DA所在直线为y轴,DD1所在直线为z轴建立空
间直角坐标系,并设C(1,0,0),则B(-1,0,0),A(0,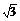 ,0),C1(1,0,2),
,0),C1(1,0,2),
∵AC的中点为F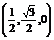 , ∴
, ∴
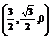 ,∴平面AC1C的法向量n1=(3,
,∴平面AC1C的法向量n1=(3,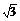 ,0).
,0).
 设平面AC1D的法向量为n2=(x,y,z), ∵
设平面AC1D的法向量为n2=(x,y,z), ∵ (0,
(0,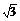 ,0),
,0),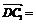 (1,0,2).
(1,0,2).
∴ ∴n2=(2,0,-1),∴cos〈n1,n2〉=
∴n2=(2,0,-1),∴cos〈n1,n2〉=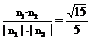
因此,二面角C-AC1-D的大小为arccos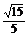 .
.
15.下面四个命题:①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥;②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥;④侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.真命题的编号是 ①④ (写出所有真命题)
9.如果三棱锥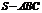 的底面是不等边三角形,侧面与底面所成的二面角相等,且顶点
的底面是不等边三角形,侧面与底面所成的二面角相等,且顶点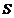 在底面的射影为
在底面的射影为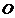 ,
,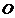 在
在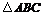 内,那么
内,那么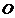 是
是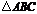 的 ( )
的 ( )
A垂心 B重心 C外心 D内心
10如图,在直三棱柱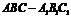 中,
中,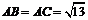 ,
, ,
,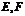 为侧棱
为侧棱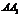 上的两点,且
上的两点,且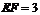 ,则多面体
,则多面体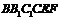 的体积等于
的体积等于
11在正方体上任意选择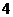 个顶点,它们可能是如下各种几何形体的
个顶点,它们可能是如下各种几何形体的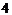 个顶点,这些几何形体是 (写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.
个顶点,这些几何形体是 (写出所有正确结论的编号).①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.
12(05上海)有两个相同的直三棱柱,高为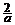 ,底面三角形的三边长分别为3a、4a,5a(
,底面三角形的三边长分别为3a、4a,5a(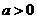 ).用它们
).用它们
拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则 的取值范围是
的取值范围是
13(07全国Ⅰ)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为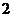 ,则该三角形的斜边长为
,则该三角形的斜边长为
14(07江苏)正三棱锥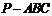 高为
高为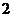 ,侧棱与底面所成角为
,侧棱与底面所成角为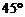 ,则点
,则点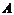 到侧面
到侧面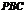 的距离是
的距离是
7.如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题是( B ) A.等腰四棱锥的腰与底面所成的角都相等 ?B.等腰四棱锥的侧面与底面所成的二面角都相等或互补
?C.等腰四棱锥的底面四边形必存在外接圆 ?D.等腰四棱锥的各顶点必在同一球面上
8一个正三棱锥与一个正四棱锥,它们的棱长都相等,把这个正三棱锥的一个侧面重合在正四棱锥的一个侧面上,这个组合体可能是 ( )
A正四棱锥 B正五棱锥 C斜三棱柱 D正三棱柱
6.正四面体A-BCD表面积为S,四个面的中心分别为E、F、G、H,设四面体E-FGH的表面积为T,则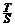 等于( A ) A.
等于( A ) A. 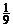 ? B.
? B. 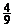 ? C.
? C. 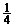 ? D.
? D. 
5.正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 (A )
A.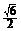 ? B.
? B.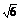 ? C.
? C.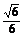 ? D.
? D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com