
4.已知正四棱柱的对角线的长为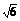 ,且对角线与底面所成角的余弦值为
,且对角线与底面所成角的余弦值为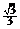 ,则该正四棱柱的体积等于 .
,则该正四棱柱的体积等于 .
典例剖析
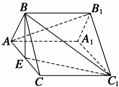 例1如图,正三棱柱ABC-A1B1C1中,E是AC中点.(1)求证:平面BEC1⊥平面ACC1A1;
例1如图,正三棱柱ABC-A1B1C1中,E是AC中点.(1)求证:平面BEC1⊥平面ACC1A1;
(2)求证:AB1∥平面BEC1; (3)若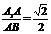 ,求二面角E-BC1-C的大小.
,求二面角E-BC1-C的大小.
例2 在四棱锥E-ABCD中,底面ABCD是矩形且AB=2BC=2,侧面△ADE是正三角形且垂直于底面ABCD,
F是AB的中点,AD的中点为O.求:(1)异面直线AE与CF所成的角;(2)点O到平面EFC的距离;
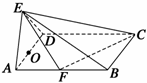 (3)二面角E-FC-D的大小.
(3)二面角E-FC-D的大小.
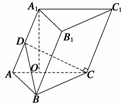 例3在三棱柱ABC-A1B1C1中,AB=
例3在三棱柱ABC-A1B1C1中,AB=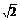 a,BC=CA=AA1=a,A1在底面ABC上的射影O在AC上.(1)求AB与侧面A1ACC1所成的角; (2)若O恰为AC的中点,求此三棱柱的侧面积.
a,BC=CA=AA1=a,A1在底面ABC上的射影O在AC上.(1)求AB与侧面A1ACC1所成的角; (2)若O恰为AC的中点,求此三棱柱的侧面积.
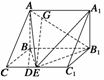
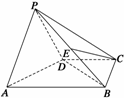 例4.如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
例4.如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=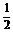 AB,E是BP的中点. (1)求证:EC∥面APD;(2)求BP与平面ABCD所成角的正切值. (3)求二面角P-AB-D的大小.
AB,E是BP的中点. (1)求证:EC∥面APD;(2)求BP与平面ABCD所成角的正切值. (3)求二面角P-AB-D的大小.
 例5如图所示,三棱锥
例5如图所示,三棱锥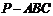 中,
中,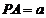 ,
,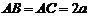 ,
,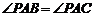
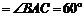 ,求三棱锥
,求三棱锥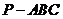 的体积.(要求用四种不同的方法)
的体积.(要求用四种不同的方法)
3.平行于棱锥底面的截面把棱锥某侧面分成面积比1∶3两部分,则棱锥的侧棱分成两部分长度比(从上到下)为 ( )
?A.1∶1 ? B.1∶3? C.1∶2? D.1∶5
|
A.棱柱有一条侧棱与底面垂直 ?B.棱柱有一条侧棱与底面的两条边垂直
? C.棱柱有一个侧面是矩形,且与底面垂直 D.棱柱有两个侧面是矩形,且与底面垂直
2.(2009·开封模拟)已知长方体的全面积为11,十二条棱长度之和为24,则这个长方体的一条对角线长为( ) ?A.2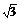 ? B.
? B.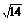 ? C.5? D.6
? C.5? D.6
4.棱锥的体积: .
3.一般棱锥的性质--定理:
棱锥被平行于棱锥底面的平面所截, .
2.正棱锥的性质:
(1)各侧棱 ,各侧面都是 .
(2) 组成一个直角三角形; 组成一个直角三角形.
1.定义: 叫棱锥.
如果一个棱锥 ,这样的棱锥叫做正棱锥.
(1)定义: 叫做棱柱.
(2) 棱柱的性质:
①侧棱 ,侧面都是 ;②两个底面与平行于底面的截面 ;
③过不相邻的两条侧棱的截面是 .
(3)棱柱的分类:①按底面多边形的边数分类:②按侧棱与底面的位置关系分类:
(4)特殊的四棱柱:
四棱柱→平行六面体→直平行六面体→长方体→正四棱柱 →正方体.请在“→”上方添上相应的条件.
(5)长方体对角线定理:
长方体的一条对角线的平方等于
(6)棱柱的体积公式:
19.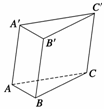 三棱柱ABC-A′B′C′的所有棱长均为a,∠A′AB=∠A′AC=60°,求其全面积.
三棱柱ABC-A′B′C′的所有棱长均为a,∠A′AB=∠A′AC=60°,求其全面积.
18.如图所示,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,AB=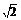 ,BB1=2,BC=1,∠BCC1=
,BB1=2,BC=1,∠BCC1=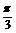 ,求:(1)异面直线AB与EB1的距离;(2)二面角A-EB1-A1的平面角的正切值.
,求:(1)异面直线AB与EB1的距离;(2)二面角A-EB1-A1的平面角的正切值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com