
2.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为 ( A )
?A.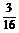 ? B.
? B.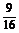 ? C.
? C.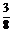 ? D.
? D.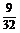
1.一个正方体内接于一个球,过球心作一截面,则截面的可能图形是 ( C )
A.①③?B.②④? C.①②③?D.②③④
4.已知正四棱柱的对角线的长为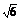 ,且对角线与底面所成角的余弦值为
,且对角线与底面所成角的余弦值为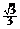 ,则该正四棱柱的体积等于 2 .
,则该正四棱柱的体积等于 2 .
典例剖析
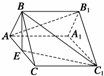
例1 如图所示,正三棱柱ABC-A1B1C1中,E是AC中点. (1)求证:平面BEC1⊥平面ACC1A1;
(2)求证:AB1∥平面BEC1; (3)若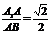 ,求二面角E-BC1-C的大小.
,求二面角E-BC1-C的大小.
 (1)证明 ∵ABC-A1B1C1是正三棱柱, ∴A1A⊥平面ABC,∴BE⊥AA1.
(1)证明 ∵ABC-A1B1C1是正三棱柱, ∴A1A⊥平面ABC,∴BE⊥AA1.
∵△ABC是正三角形,E是AC的中点, ∴BE⊥AC,又AA1∩AC=A,∴BE⊥平面ACC1A1,
又∵BE 平面BEC1, ∴平面BEC1⊥平面ACC1A1.
平面BEC1, ∴平面BEC1⊥平面ACC1A1.
(2)证明 连结B1C,设BC1∩B1C=D,连结DE.
∵ABC-A1B1C1是正三棱柱, ∴BCC1B1是矩形,D是B1C的中点.
∵E是AC的中点,∴AB1∥DE.∵DE 平面BEC1,AB1
平面BEC1,AB1 平面BEC1, ∴AB1∥平面BEC1.
平面BEC1, ∴AB1∥平面BEC1.
(3)解 作CF⊥EC1于F, 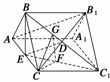 FG⊥BC1于G,连结CG. ∵平面BEC1⊥平面ACC1A1,
FG⊥BC1于G,连结CG. ∵平面BEC1⊥平面ACC1A1,
∴CF⊥平面BEC1. ∴FG是CG在平面BEC1上的射影.根据三垂线定理得,CG⊥BC1.
∴∠CGF是二面角E-BC1-C的平面角. 设AB=a,∵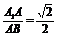 ,则AA1=
,则AA1=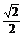 a.
a.
在Rt△ECC1中,CF=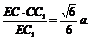 在Rt△BCC1中,CG=
在Rt△BCC1中,CG=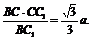
在Rt△CFG中, ∵sin∠CGF=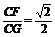 ,∴∠CGF=45°. ∴二面角E-BC1-C的大小为45°.
,∴∠CGF=45°. ∴二面角E-BC1-C的大小为45°.
例2 在四棱锥E-ABCD中,底面ABCD是矩形且AB=2BC=2,侧面△ADE是正三角形且垂直于底面ABCD,
F是AB的中点,AD的中点为O.求:(1)异面直线AE与CF所成的角;(2)点O到平面EFC的距离;
(3)二面角E-FC-D的大小.
解 (1)取EB的中点G,连结FG,则FG∥AE,∴∠GFC为AE与CF所成的角,
∵平面AED⊥平面ABCD,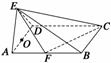 ∴底面ABCD是矩形,∴AB⊥AD,
∴底面ABCD是矩形,∴AB⊥AD,
∴AB⊥平面EAD,∴AB⊥EA, ∴EB=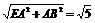 同理,EC=
同理,EC=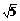 .
.
 ∴在△EBC中,由余弦定理得CG=
∴在△EBC中,由余弦定理得CG=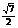 . 又∵FG=
. 又∵FG=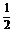 EA=
EA=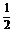 ,CF=
,CF=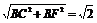 .
.
∴△CFG是直角三角形, ∴cos∠CFG=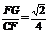 ,∴异面直线AE与CF所成的角为arccos
,∴异面直线AE与CF所成的角为arccos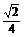 .
.
(2)AD的中点为O,则EO⊥平面ABCD, 作OR⊥CF且与CF交于点R,则CF⊥ER
∴CF⊥平面EOR,又∵CF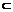 平面EFC, ∴平面EOR⊥平面EFC.
平面EFC, ∴平面EOR⊥平面EFC.
过O作OH⊥ER且与ER交于H, 则OH⊥平面EFC,
∴OH的长即为点O到平面EFC的距离. 由S△CFO=S矩形ABCD-S△AOF-S△CBF-S△COD,∴OR=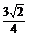 .
.
在Rt△EOR中,OH=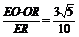 .∴所求距离为
.∴所求距离为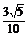 .
.
(3)∠ERO即为二面角E-FC-D的平面角, an∠ERO=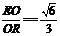 ∴所求二面角的大小是arctan
∴所求二面角的大小是arctan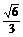 .
.
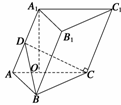 例3在三棱柱ABC-A1B1C1中,AB=
例3在三棱柱ABC-A1B1C1中,AB= a,BC=CA=AA1=a,A1在底面ABC上的射影O在AC上.
a,BC=CA=AA1=a,A1在底面ABC上的射影O在AC上.
(1)求AB与侧面A1ACC1所成的角; (2)若O恰为AC的中点,求此三棱柱的侧面积.
解 (1)∵A1O⊥平面ABC, ∴平面A1ACC1⊥平面ABC.
在△ABC中,由BC=AC=a, AB= a,
a,
得∠ACB=90°,∠CAB=45°,∴BC⊥AC,∴BC⊥平面A1ACC1, AB与侧面A1ACC1所成的角为∠CAB=45°. (2)O是AC中点, 在Rt△AA1O中, AA1=a,AO=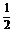 a, ∴∠A1AC=60°,
a, ∴∠A1AC=60°,
过C作CD⊥CC1交AA1于D,连结BD,由(1)知BC⊥平面A1ACC1,
∴BC⊥CC1,又BC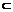 平面BCD, CD
平面BCD, CD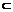 平面BCD,BC∩CD=C,∴CC1⊥截面BCD,∴CC1⊥BD,
平面BCD,BC∩CD=C,∴CC1⊥截面BCD,∴CC1⊥BD,
∴AA1⊥BD, 在Rt△ACD中,CD= a,在Rt△BCD中,BD=
a,在Rt△BCD中,BD=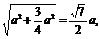
则S三棱柱侧=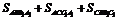 ?=AA1·BD+AA1·DC+CC1·BC=
?=AA1·BD+AA1·DC+CC1·BC=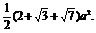
例4.如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=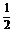 AB,E是BP的中点. (1)求证:EC∥面APD;(2)求BP与平面ABCD所成角的正切值. (3)求二面角P-AB-D的大小. (1)证明 如图,取PA中点F,连结EF、FD, ∵E是BP的中点,
AB,E是BP的中点. (1)求证:EC∥面APD;(2)求BP与平面ABCD所成角的正切值. (3)求二面角P-AB-D的大小. (1)证明 如图,取PA中点F,连结EF、FD, ∵E是BP的中点,
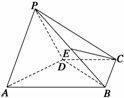 ∴EF∥AB且EF=
∴EF∥AB且EF=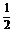 AB. 又∵DC∥AB,DC=
AB. 又∵DC∥AB,DC=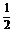 AB, ∴EF∥CD且EF=CD.
AB, ∴EF∥CD且EF=CD.
∴四边形EFDC是平行四边形,故得EC∥FD.
又∵EC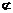 平面PAD, FD
平面PAD, FD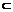 平面PAD,∴EC∥平面ADP.
平面PAD,∴EC∥平面ADP.
(2)解 取AD的中点H,连结PH,BH, ∵PA=PD,∴PH⊥AD.
∵平面PAD⊥平面ABCD,∴PH⊥平面ABCD.
∴HB是PB在平面ABCD内的射影. ∴∠PBH是PB与平面ABCD所成的角.
由已知∠ABC=∠BCD=90°, 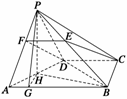 ∴四边形ABCD是直角梯形,DC=CB=
∴四边形ABCD是直角梯形,DC=CB=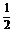 AB.
AB.
设AB=2a,则BD= a, 在△ADB中,易得∠DBA=45°,∴AD=
a, 在△ADB中,易得∠DBA=45°,∴AD= a.
a.
PH= .又∵BD2+AD2=4a2=AB2,
.又∵BD2+AD2=4a2=AB2,
∴△ABD是等腰直角三角形,∠ADB=90°.∴HB=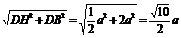 .
.
∴在Rt△PHB中,tan∠PBH=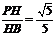 .
.
(3)解 在平面ABCD内过点H作AB的垂线交AB于G点,连结PG,则HG是PG在平面ABCD内的射影,
故PG⊥AB,所以∠PGH是二面角P-AB-D的平面角,
由AB=2a,HA=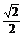 a,又∠HAB=45°,∴HG=
a,又∠HAB=45°,∴HG=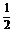 a. 在Rt△PHG中,tan∠PGH=
a. 在Rt△PHG中,tan∠PGH=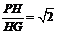 .
.
∴二面角P-AB-D的大小为arctan .
.
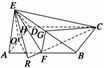
例5如图所示,三棱锥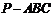 中,
中,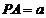 ,
,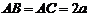 ,
,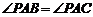
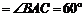 ,
, 求三棱锥
求三棱锥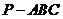 的体积.(要求用四种不同的方法)
的体积.(要求用四种不同的方法)
3.平行于棱锥底面的截面把棱锥某侧面分成面积比1∶3两部分,则棱锥的侧棱分成两部分长度比(从上到下)为 ( A )
?A.1∶1 ? B.1∶3? C.1∶2? D.1∶5
|
A.棱柱有一条侧棱与底面垂直 ?B.棱柱有一条侧棱与底面的两条边垂直
? C.棱柱有一个侧面是矩形,且与底面垂直 D.棱柱有两个侧面是矩形,且与底面垂直
2.(2009·开封模拟)已知长方体的全面积为11,十二条棱长度之和为24,则这个长方体的一条对角线长为(C ) ?A.2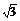 ? B.
? B.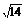 ? C.5? D.6
? C.5? D.6
4.棱锥的体积: V=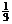 Sh,其S是棱锥的底面积,h是高.
Sh,其S是棱锥的底面积,h是高.
3.一般棱锥的性质--定理:
棱锥被平行于棱锥底面的平面所截,则截面和底面相似,且其面积的比等于截得的棱锥的高和已知棱锥高的平方比.
2.正棱锥的性质:
(1)各侧棱相等,各侧面都是全等的等腰三角形.
(2)棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形.
1.定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥.
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,这样的棱锥叫做正棱锥.
(1)定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.
(2) 棱柱的性质:
①侧棱都相等,侧面都是平行四边形;②两个底面与平行于底面的截面是全等的多边形;
③过不相邻的两条侧棱的截面是平行四边形.
(3)棱柱的分类:
①按底面多边形的边数分类:②按侧棱与底面的位置关系分类:
(4)特殊的四棱柱:
四棱柱→平行六面体→直平行六面体→长方体→正四棱柱 →正方体.请在“→”上方添上相应的条件.
(5)长方体对角线定理:
长方体的一条对角线的平方等于一个顶点上三条棱的长的平方和.
(6)棱柱的体积公式: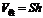 ,
,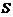 是棱柱的底面积,
是棱柱的底面积,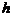 是棱柱的高.
是棱柱的高.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com