
5.一个棱长都为a的正三棱柱的六个顶点全部在同一个球面上,则此球的表面积为 ( )
A.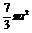 B.
B.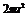 ? C.
? C.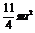 D.
D.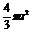
4.在底面边长为6 cm,高为14 cm的正三棱柱内放入相同的n个球,使球半径尽量大,则n的值为 ( )
A.4? B.5? C.6? D.7
3.在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若侧棱SA=2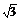 ,则正棱锥S-ABC外接球的表面积是 (
)
,则正棱锥S-ABC外接球的表面积是 (
)
A.12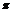 ? B.32
? B.32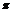 ? C.36
? C.36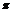 ? D.48
? D.48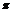
2.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为 ( )
?A.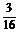 ? B.
? B.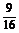 ? C.
? C. ? D.
? D.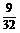
1.一个正方体内接于一个球,过球心作一截面,则截面的可能图形是 ( )
A.①③?B.②④? C.①②③?D.②③④
18.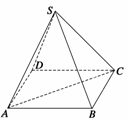 如图所示,已知正四棱锥S-ABCD中,底面边长为a,侧棱长为
如图所示,已知正四棱锥S-ABCD中,底面边长为a,侧棱长为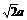 .(1)求它的外接球的体积;(2)求它的内切球的表面积.
.(1)求它的外接球的体积;(2)求它的内切球的表面积.
解 (1)设外接球的半径为R,球心为O,则OA=OC=OS,
所以O为△SAC的外心,即△SAC的外接圆半径就是球的半径.
∵AB=BC=a,∴AC=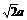 .∵SA=SC=AC=
.∵SA=SC=AC=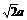 , ∴△SAC为正三角形.
, ∴△SAC为正三角形.
由正弦定理得2R=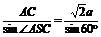 =
=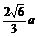 , 因此,R=
, 因此,R= ,
,
V球=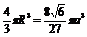 .
.
(2)设内切球半径为r,作SE⊥底面ABCD于E,
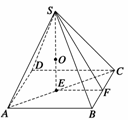 作SF⊥BC于F,连结EF,
作SF⊥BC于F,连结EF,
则有SF=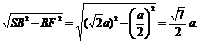
S△SBC=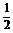 BC·SF=
BC·SF=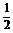 a×
a×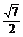 a=
a=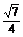 a2,
a2,
S棱锥全=4S△SBC+S底=(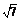 +1)a2.
+1)a2.
又SE=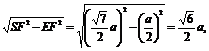
∴V棱锥=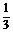 S底h=
S底h=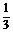 a2×
a2×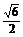 a=
a=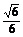 a3,
a3,
∴r=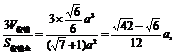
S球=4 r2=
r2=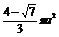 .
.
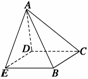
17.如图四棱锥A-BCDE中,AD⊥底面BCDE,AC⊥BC,AE⊥BE. (1)求证: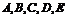 五点共球;
五点共球;
(2)若∠CBE=90°,CE=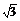 ,AD=1,求B、D两点的球面距离.
,AD=1,求B、D两点的球面距离.
(1)证明 取AB的中点P,连接PE,PC,PD,由题设条件知△AEB、△ADB、△ABC都是直角三角形.
 故PE=PD=PC=
故PE=PD=PC=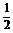 AB=PA=PB. 所以A、B、C、D、E五点在同一球面上.
AB=PA=PB. 所以A、B、C、D、E五点在同一球面上.
(2)解 由题意知四边形BCDE为矩形, 所以BD=CE=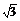 ,
,
在Rt△ADB中,AB=2,AD=1, ∴∠DPB=120°,D、B的球面距离为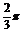 .
.
16.已知A、B、C是半径为1的球面上的三点,B、C两点间的球面距离为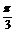 ,点A与B、C两点间的球面距离均为
,点A与B、C两点间的球面距离均为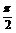 ,且球心为O.求: (1)∠BOC、∠AOB的大小;(2)球心到截面ABC的距离.
,且球心为O.求: (1)∠BOC、∠AOB的大小;(2)球心到截面ABC的距离.
解 (1)∠BOC=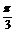 ,∠AOB==
,∠AOB==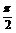 .
.
(2)连结OA、OB、OC、AB、AC、BC得三棱锥O-ABC,设OH⊥平面ABC,H为垂足,则h=OH为球心到截面ABC的距离,由OA⊥OB,OA⊥OC得OA⊥平面OBC,VA-OBC=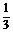 ·S△OBC=
·S△OBC=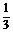 ×
×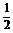 ×1×1×sin60°=
×1×1×sin60°=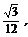
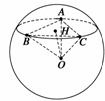 在△ABC中,AB=AC=
在△ABC中,AB=AC=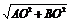 =
=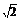 ,BC=1, 底边BC的高为
,BC=1, 底边BC的高为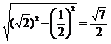 .
.
又VO-ABC=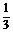 hS△ABC=
hS△ABC=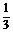 ·h·
·h·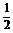 ×
×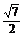 ×1, 故
×1, 故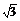 =
=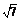 h,即h=
h,即h=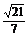 .
.
15.各个顶点在一个直径为2 cm的球面上.如果正四棱柱的底面边长为1 cm,那么该棱柱的表面积为 2+4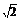 cm2.
cm2.
14.(2008·安徽)已知点A、B、C、D在同一个球面上,AB⊥平面BCD,BC⊥CD,若AB=6,AC=2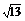 ,AD=8,
,AD=8,
则B、C两点间的球面距离是  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com