
7. 球的表面积和体积公式:
球的表面积和体积公式: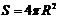 ,
,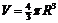 .
.
6.两点的球面距离:经过两点的大圆在这两点间的一段劣弧的长度,叫做两点的球面距离. (
(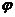 为球心角的弧度数).
为球心角的弧度数).
5.球的性质:
(1)平面截球所得的截面是圆. 球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆。
(2)球心和球面圆心的连线垂直于截面;
(3)球心到截面的距离d与球的半径R及截面的半径r的关系: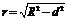
(4)地球上的径度是个二面角,纬度是个线面角。
4. 球的概念: 与定点距离等于或小于定长的点的集合,叫做球体,简称球 定点叫球心,定长叫球的半径
定点叫球心,定长叫球的半径 与定点距离等于定长的点的集合叫做球面.一个球或球面用球心的字母表示。
与定点距离等于定长的点的集合叫做球面.一个球或球面用球心的字母表示。
3.简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面.如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体.
说明:棱柱、棱锥、正多面体等一切凸多面体都是简单多面体
2.正多面体有且只有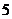 种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.
种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.
1.每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体.
4. 若三棱锥的三个侧面两两垂直,且侧棱长均为
若三棱锥的三个侧面两两垂直,且侧棱长均为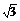 ,则其外接球的表面积是 .
,则其外接球的表面积是 .
典例剖析
例1 已知在多面体ABCDEFG中,AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,
平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则这个多面体的体积为 ( )
?A.2 ?B.4 C.6 D.8
例2①已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,则球的半径等于 ,球的表面积等于 .
②设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是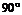 ,且二面角B-OA-C的大小为
,且二面角B-OA-C的大小为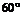 ,则从A点沿球面经B、C两点再回到A点的最短距离是( ? )
,则从A点沿球面经B、C两点再回到A点的最短距离是( ? )
?A.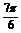 ? B.
? B.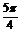 ? C.
? C.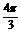 ? D.
? D.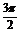
例3①P、Q为斜三棱柱相对棱上的点,若AQ=PC1,则多面体B-ACPQ的体积是三棱柱体积的 ( )
?A.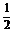 ? B.
? B.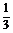 ? C.
? C.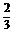 ? D.
? D.
②设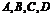 是球面上的四个点,且共面,AB=BC=CD=DA=3,球心到该面距离是球半径的一半,则球的体积是( )
是球面上的四个点,且共面,AB=BC=CD=DA=3,球心到该面距离是球半径的一半,则球的体积是( )
?A.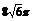 ? B.
? B.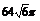 ? C.
? C.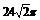 ? D.
? D.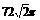
③长方体ABCD-A1B1C1D1的8个顶点在同一个球面上,且AB=2,AD=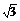 ,AA1=1,则顶点A、B间的球面距离是 ( )?A.
,AA1=1,则顶点A、B间的球面距离是 ( )?A.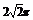 ? B.
? B.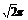 ? C.
? C.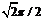 ? D.
? D.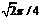
④长方体ABCD-A1B1C1D1的各顶点都在球O的球面上,其中AB∶AD∶AA1=1∶1∶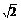 ,A、B两点的球面距离记为m,A、D1两点的球面距离记为n,则
,A、B两点的球面距离记为m,A、D1两点的球面距离记为n,则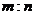 的值为 .
的值为 .
例4已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC、△PEF都是正三角形,PF⊥AB.
(1)证明:PC⊥平面PAB; (2)求二面角P-AB-C的平面角的余弦值;
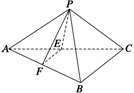 (3)若点P、A、B、C在一个表面积为12
(3)若点P、A、B、C在一个表面积为12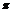 的球面上,求△ABC的边长.
的球面上,求△ABC的边长.
例4如图,三个12×12 cm的正方形,都被连结相邻两边中点的直线分成A、B两片(如图(1)),把6片粘在一个正六边形的外面(如图(2)),然后折成多面体(如图(3)),求此多面体的体积.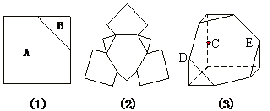
例5已知球的半径为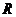 ,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
3.球面上有三点,任意两点的球面距离都等于大圆周长的1/6,经过这三个点的小圆周长为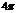 ,那么这个球的半径为(B)
,那么这个球的半径为(B)
?A.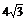 B.
B.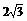 ?
C.2? D.
?
C.2? D.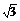
2.把边长为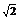 的正方形ABCD沿对角线AC折成直二面角,折成直二面角后,在A,B,C,D四点所在的球面上,
的正方形ABCD沿对角线AC折成直二面角,折成直二面角后,在A,B,C,D四点所在的球面上,
B与D两点之间的球面距离为 (
) ?A.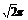 B.
B.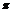 C.
C.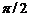 ? D.
? D.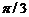
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com