
6、向量法:
例8 、设 ,
, 为直角坐标平面内
为直角坐标平面内 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量 ,
,
 ,且
,且 . (1)求点
. (1)求点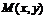 的轨迹
的轨迹 的方程;
的方程;
(2)过点(0,3)作直线 与曲线
与曲线 交于
交于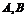 两点,设
两点,设 ,是否存在这样的直线
,是否存在这样的直线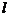 ,使得四边形
,使得四边形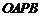 是矩形?若存在,求出直线
是矩形?若存在,求出直线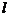 的方程;若不存在,试说明理由。
的方程;若不存在,试说明理由。
例9、设点A和B为抛物线 (p>0)上原点以外的两个动点,已知OA⊥OB,OM⊥AB,求点M的轨迹方程,并说明它表示什么曲线。
(p>0)上原点以外的两个动点,已知OA⊥OB,OM⊥AB,求点M的轨迹方程,并说明它表示什么曲线。
沙城中学补习班数学第一轮复习学案 编录:刘世亮
轨迹方程作业
5、交轨法;它常常适用于出现需求两曲线交点的轨迹方程问题 ,解此类问题往往需借助解方程组得出含有某参数的交点坐标,再消去参数而得到所求动点的轨迹方程。
例7、抛物线 的顶点作互相垂直的两弦OA、OB,求抛物线的顶点O在直线AB上的射影M的轨迹。
的顶点作互相垂直的两弦OA、OB,求抛物线的顶点O在直线AB上的射影M的轨迹。
4、引参消参法; 若题目出现当动点运动所受限制条件较多,不易直接建立x、y的某种联系,但且发现x、y同时受到另外一个变量t(如角度、斜率、截距等)的制约而将它们用t表示,然后通过消去变量t而得到所要求的动点的轨迹方程f(x, y)=0。
例6、过点M(-2,
0)作直线L交双曲线 于A、B两点,以OA、OB为邻边作平行四边形OAPB。求动点P的轨迹方程。
于A、B两点,以OA、OB为邻边作平行四边形OAPB。求动点P的轨迹方程。
3、相关点法;若动点P(x, y)依赖于某已知曲线上的另一个动点P (x
(x ,y
,y )而运动,且x
)而运动,且x , y
, y 可用x, y表示,则将P
可用x, y表示,则将P (x
(x ,y
,y )代入已知曲线,求出P点的轨迹方程。此法也称代入法或转移法。
)代入已知曲线,求出P点的轨迹方程。此法也称代入法或转移法。
例4、定点A(3,0)为圆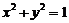 外一定点,P为圆上任一点,(除出圆与x轴的交点), ∠POA的平分线交PA于点Q, 求出Q点的轨迹方程。
外一定点,P为圆上任一点,(除出圆与x轴的交点), ∠POA的平分线交PA于点Q, 求出Q点的轨迹方程。
例5.如图所示,过椭圆E: 上任一点P,作右准线
上任一点P,作右准线 的垂线PH,垂足为H。延长PH到Q,使
的垂线PH,垂足为H。延长PH到Q,使 (1)当P点在E上运动时,求点Q的轨迹G的方程;(2)当
(1)当P点在E上运动时,求点Q的轨迹G的方程;(2)当 取何值时,轨迹G是焦点在平行于
取何值时,轨迹G是焦点在平行于 轴的直线上的椭圆?证明这些焦点都在同一个椭圆
轴的直线上的椭圆?证明这些焦点都在同一个椭圆 上,并写出椭圆的方程;(3)当
上,并写出椭圆的方程;(3)当 取何值时,轨迹G是一个圆?判断这个圆与椭圆
取何值时,轨迹G是一个圆?判断这个圆与椭圆 的右准线
的右准线 的位置关系。
的位置关系。
2、定义法;若动点轨迹直接符合已知圆锥曲线定义,则可直接利用定义写出其方程。
例2、已知定点A(0,7)、B(0,-7)、C(12,2),以C为一个焦点作过A、B的椭圆,求另一焦点F的轨迹方程.
例3、已知圆O: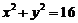 及点A(2, 0),求过A且与圆O相切的诸圆圆心P的轨迹方程。
及点A(2, 0),求过A且与圆O相切的诸圆圆心P的轨迹方程。
1、直译解析法;该方法的主要思路就是将题目中的几何条件直接翻译为代数条件。它主要通过建系、设点、列式、化简、讨论等步骤得到所求的曲线轨迹方程。
例1设动直线 垂直于
垂直于 轴,且与椭圆
轴,且与椭圆 交于
交于 两点,P是
两点,P是 上满足
上满足 的点,求点P的轨迹方程。
的点,求点P的轨迹方程。
4. 若三棱锥的三个侧面两两垂直,且侧棱长均为
若三棱锥的三个侧面两两垂直,且侧棱长均为 ,则其外接球的表面积是
,则其外接球的表面积是  .
.
典例剖析
例1 已知在多面体ABCDEFG中,AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,
平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则这个多面体的体积为 ( B )
?A.2 ?B.4 C.6 D.8
例2①已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,则球的半径等于  ,球的表面积等于 54
,球的表面积等于 54 .
.
②设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是 ,且二面角B-OA-C的大小为
,且二面角B-OA-C的大小为 ,则从A点沿球面经B、C两点再回到A点的最短距离是(C? )
,则从A点沿球面经B、C两点再回到A点的最短距离是(C? )
?A.? B.
B.  ? C.
? C.  ? D.
? D. 
例3①P、Q为斜三棱柱相对棱上的点,若AQ=PC1,则多面体B-ACPQ的体积是三棱柱体积的 ( B )
?A. ? B.
? B.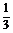 ? C.
? C.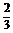 ? D.
? D.
②设A、B、C、D是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,球心到该平面的距离是球半径的一半,则球的体积是 ( A )
?A. ? B.
? B. ? C.
? C. ? D.
? D.
③长方体ABCD-A1B1C1D1的8个顶点在同一个球面上,且AB=2,AD= ,AA1=1,则顶点A、B间的球面距离是 ( C )?A.
,AA1=1,则顶点A、B间的球面距离是 ( C )?A. ? B.
? B. ? C.
? C.
 ? D.
? D.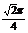
④长方体ABCD-A1B1C1D1的各顶点都在球O的球面上,其中AB∶AD∶AA1=1∶1∶ ,A、B两点的球面距离记为m,A、D1两点的球面距离记为n,则
,A、B两点的球面距离记为m,A、D1两点的球面距离记为n,则 的值为 1:2 .
的值为 1:2 .
例4已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC、△PEF都是正三角形,PF⊥AB.
(1)证明:PC⊥平面PAB; (2)求二面角P-AB-C的平面角的余弦值;
 (3)若点P、A、B、C在一个表面积为12
(3)若点P、A、B、C在一个表面积为12 的球面上,求△ABC的边长.
的球面上,求△ABC的边长.
(1)证明 连结CF,∵PE=EF = BC=
BC= AC,∴AP⊥PC.
AC,∴AP⊥PC.
∵CF⊥AB,PF⊥AB, CF∩PF=F. ∴AB⊥平面PCF.
∵PC 平面PCF, ∴PC⊥AB. 又∵AP∩AB=A, ∴PC⊥平面PAB.
平面PCF, ∴PC⊥AB. 又∵AP∩AB=A, ∴PC⊥平面PAB.
(2)方法一 ∵AB⊥PF,AB⊥CF, ∴∠PFC为所求二面角的平面角.
 设AB=a,则PF=EF=
设AB=a,则PF=EF= ,CF=
,CF= . ∴cos∠PFC=
. ∴cos∠PFC= .
.
方法二 设P在平面ABC内的射影为O. ∵△PAF≌△PAE,∴△PAB≌△PAC,
得PA=PB=PC,于是O是△ABC的中心. ∴∠PFO为所求二面角的平面角.
设AB=a,则PF= ,OF=
,OF=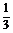 ·
· . ∴cos∠PFO=
. ∴cos∠PFO= .
.
(3)方法一 设PA=x,球半径为R. ∵PC⊥平面PAB,PA⊥PB,∴ =2R.
=2R.
∵ =
= ,∴R=
,∴R= ,得x=2. ∴△ABC的边长为
,得x=2. ∴△ABC的边长为 .
.
方法二延长PO交球面于D,则PD是球的直径.连结OA、AD,得△PAD为直角三角形,设AB=x,球半径为R. ∵ =
= ,∴PD=
,∴PD=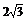 , ∵PO=OFtan∠PFO=
, ∵PO=OFtan∠PFO= ,OA=
,OA= ,
,
∴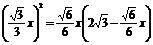 ,于是x=2
,于是x=2 . ∴△ABC的边长为2
. ∴△ABC的边长为2 .
.
例4如图,三个12×12 cm的正方形,都被连结相邻两边中点的直线分成A、B两片(如图(1)),把6片粘在一个正六边形的外面(如图(2)),然后折成多面体(如图(3)),求此多面体的体积.
解法一: 补成一个正方体,如图甲,V= V正方体=
V正方体= ×123=864 cm3.
×123=864 cm3.

甲 乙
解法二:补成一个三棱锥,如图乙,V=V大三棱锥-3V小三棱锥=864 cm3.
解法三:如图(3)7设C是所在棱的中点,截面CDE把几何体截成两部分,沿DE把上部分翻转过来可拼成正方体的下一半.
例5已知球的半径为 ,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
3.球面上有三点,任意两点的球面距离都等于大圆周长的1/6,经过这三个点的小圆周长为 ,那么这个球的半径为(B)
,那么这个球的半径为(B)
?A. B.
B.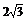 ?
C.2? D.
?
C.2? D.
2.把边长为 的正方形ABCD沿对角线AC折成直二面角,折成直二面角后,在A,B,C,D四点所在的球面上,
的正方形ABCD沿对角线AC折成直二面角,折成直二面角后,在A,B,C,D四点所在的球面上,
B与D两点之间的球面距离为 (
C ) ?A. B.
B. C.
C.  ? D.
? D.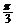
1.正方体的全面积为24,球O与正方体的各棱均相切,球O的体积是 ( D )
?
A. ?
B.
?
B. ?
C.
?
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com