
16.设函数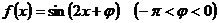 ,该图象的一个对称中心为
,该图象的一个对称中心为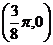
(1)求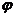
(2)求函数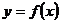 的单调增区间
的单调增区间
15.(1)已知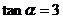 求
求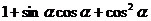 的值
的值
(2)证明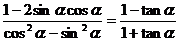
14.给出下列命题
(1)函数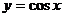 在第三、四象限都是增函数。
在第三、四象限都是增函数。
(2)函数 的最小正周期为
的最小正周期为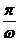
(3)函数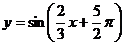 是偶函数
是偶函数
(4)函数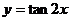 的图象向左平移
的图象向左平移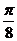 个单位长度得
个单位长度得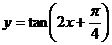 的图象
的图象
其中正确的有 (将正确答案的序号填在横线上)。
13.若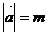 ,
,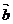 与
与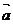 的方向相反,且
的方向相反,且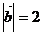 ,则
,则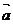 =
(用
=
(用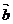 来表示)
来表示)
12.函数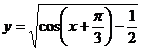 的定义域为
的定义域为
11.函数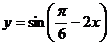 的单调递减区间是
的单调递减区间是
22.(本小题满分14分)
对于正整数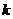 ,用
,用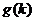 表示
表示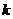 的最大奇因数,如:
的最大奇因数,如: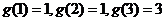 ,……. 记
,……. 记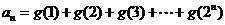 ,其中
,其中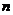 是正整数.
是正整数.
(I)写出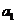 ,
,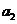 ,
,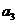 ,并归纳猜想
,并归纳猜想 与
与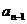
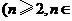 N)的关系式;
N)的关系式;
(II)证明(I)的结论;
(Ⅲ)求 的表达式.
的表达式.
21.(本小题满分12分)
已知点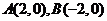 ,
,
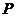 是平面内一动点,直线
是平面内一动点,直线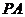 、
、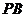 斜率之积为
斜率之积为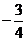 .
.
(Ⅰ)求动点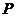 的轨迹
的轨迹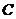 的方程;
的方程;
(Ⅱ)过点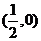 作直线
作直线 与轨迹
与轨迹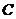 交于
交于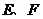 两点,线段
两点,线段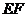 的中点为
的中点为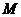 ,求直线
,求直线 的斜率
的斜率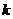 的取值范围.
的取值范围.
20.(本小题满分12分)
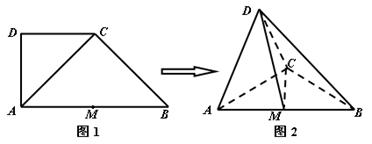
如图1,在直角梯形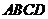 中,
中, ,
, ,
, ,
, 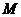 为线段
为线段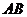 的中点.将
的中点.将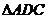 沿
沿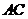 折起,使平面
折起,使平面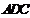
 平面
平面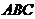 ,得到几何体
,得到几何体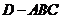 ,如图2所示.
,如图2所示.
(Ⅰ) 求证: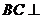 平面
平面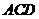 ;
;
(Ⅱ) 求二面角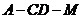 的余弦值.
的余弦值.
19.(本小题满分12分)
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定
正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是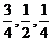 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为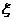 ,求
,求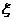 的分布列、数学期望和方差.
的分布列、数学期望和方差.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com