
2.在等差数列{a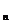 }中,已知a
}中,已知a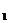 =2,a
=2,a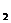 +a
+a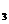 =13,则a
=13,则a +a
+a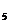 +a
+a 等于
等于
A.40 B.42 C.43 D.45
1.如果-1,a, b,c,-9成等比数列,那么
A.b=3,ac=9 B.b=-3,ac=9 C.b=3,ac=-9 D.b=-3,ac=-9
12. (全国卷III) 在等差数列 中,公差
中,公差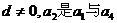 的等比中项.
的等比中项.
已知数列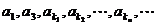 成等比数列,求数列
成等比数列,求数列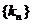 的通项
的通项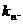
解:由题意得: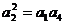 ……………1分
……………1分
即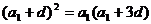 …………3分
…………3分
又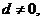
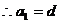 …………4分
…………4分
又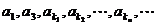 成等比数列,
成等比数列,
∴该数列的公比为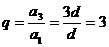 ,………6分
,………6分
所以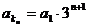 ………8分
………8分
又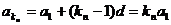 ……………………………………10分
……………………………………10分
 所以数列
所以数列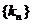 的通项为
的通项为 ……………………………12分
……………………………12分
课后训练:
11.(福建卷)已知数列{an}满足a1=a, an+1=1+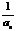 我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
(Ⅰ)求当a为何值时a4=0;(Ⅱ)设数列{bn}满足b1=-1, bn+1=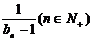 ,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
(I)解法一: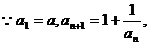
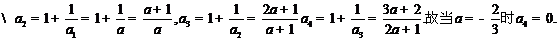
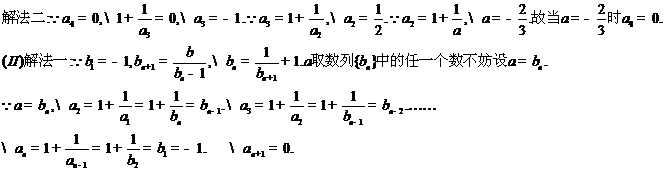 故a取数列{bn}中的任一个数,都可以得到一个有穷数列{an}
故a取数列{bn}中的任一个数,都可以得到一个有穷数列{an}
10.(安徽卷)数列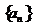 的前
的前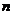 项和为
项和为 ,已知
,已知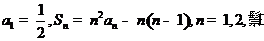
(Ⅰ)写出 与
与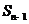 的递推关系式
的递推关系式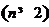 ,并求
,并求 关于
关于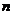 的表达式;
的表达式;
(Ⅱ)设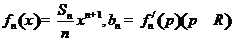 ,求数列
,求数列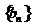 的前
的前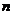 项和
项和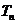 。
。
解:由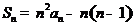
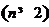 得:
得: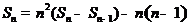 ,即
,即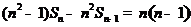 ,所以
,所以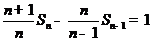 ,对
,对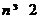 成立。
成立。
由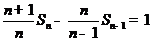 ,
,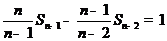 ,…,
,…,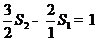 相加得:
相加得: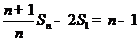 ,又
,又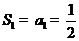 ,所以
,所以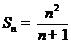 ,当
,当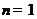 时,也成立。
时,也成立。
(Ⅱ)由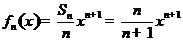 ,得
,得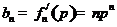 。
。
而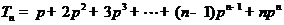 ,
,
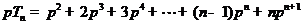 ,
,
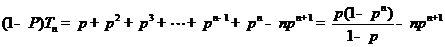
9.根据流程图,(1)求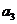 ;(2)若
;(2)若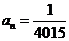 ,求n.
,求n.
[问题6]数列创新题
8. 数列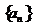 的前
的前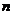 项和为
项和为 =n2+2n-1,试用程序框图
=n2+2n-1,试用程序框图
表示数列通项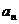 的过程,并写出数列的前5项和通项公式
的过程,并写出数列的前5项和通项公式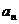 .
.
7.已知抛物线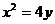 ,过原点作斜率1的直线交抛物线于第一象限内一点
,过原点作斜率1的直线交抛物线于第一象限内一点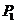 ,又过点
,又过点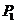 作斜率为
作斜率为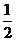 的直线交抛物线于点
的直线交抛物线于点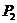 ,再过
,再过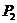 作斜率为
作斜率为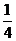 的直线交抛物线于点
的直线交抛物线于点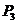 ,
,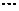 ,如此继续,一般地,过点
,如此继续,一般地,过点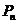 作斜率为
作斜率为 的直线交抛物线于点
的直线交抛物线于点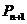 ,设点
,设点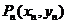 .
.
(Ⅰ)令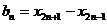 ,求证:数列
,求证:数列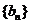 是等比数列.并求数列
是等比数列.并求数列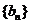 的前
的前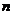 项和为
项和为
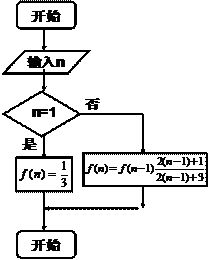 解:(1)因为
解:(1)因为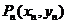 、
、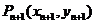 在抛物线上,故
在抛物线上,故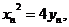 ①
①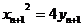 ②,又因为直线
②,又因为直线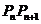 的斜率为
的斜率为 ,即
,即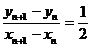 ,①②代入可得
,①②代入可得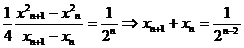
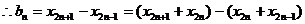
 , 故
, 故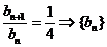 是以
是以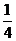
为公比的等比数列; ,
,
[问题5]数列与算法
6.(湖北卷)设数列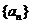 的前n项和为
的前n项和为 ,点
,点 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。
(Ⅰ)求数列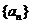 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设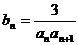 ,
,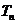 是数列
是数列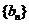 的前n项和,求使得
的前n项和,求使得 对所有
对所有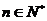 都成立的最小正整数m。
都成立的最小正整数m。
本小题主要是考查等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题能力和推理能力。
解:(I)依题意得,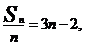 即
即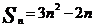 。
。
当n≥2时,a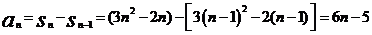 ;
;
当n=1时,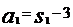 ×
×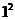 -2×1-1-6×1-5
-2×1-1-6×1-5
所以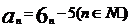 。
。
(II)由(I)得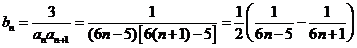 ,
,
故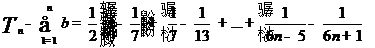 =
=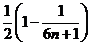 。
。
因此,使得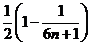 ﹤
﹤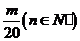 成立的m必须满足
成立的m必须满足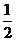 ≤
≤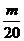 ,即m≥10,故满足要求的最小整数m为10。
,即m≥10,故满足要求的最小整数m为10。
[问题4]数列与解析几何
数列与解析几何综合题,是今后高考命题的重点内容之一,求解时要充分利用数列、解析几何的概念、性质,并结合图形求解.
例3.在直角坐标平面上有一点列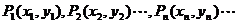 ,对一切正整数
,对一切正整数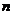 ,点
,点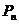 位于函数
位于函数 的图象上,且
的图象上,且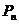 的横坐标构成以
的横坐标构成以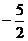 为首项,
为首项,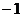 为公差的等差数列
为公差的等差数列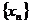 .
.
⑴求点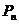 的坐标;子⑵设抛物线列
的坐标;子⑵设抛物线列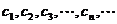 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于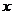 轴,第
轴,第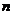 条抛物线
条抛物线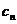 的顶点为
的顶点为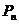 ,且过点
,且过点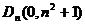 ,记与抛物线
,记与抛物线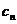 相切于
相切于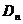 的直线的斜率为
的直线的斜率为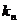 ,求:
,求: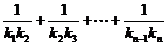 .
.
解:(1)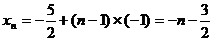
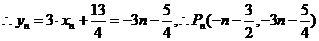
(2)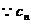 的对称轴垂直于
的对称轴垂直于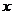 轴,且顶点为
轴,且顶点为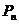 .
. 设
设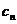 的方程为:
的方程为: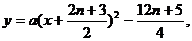
把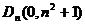 代入上式,得
代入上式,得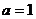 ,
,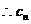 的方程为:
的方程为: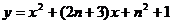 。
。
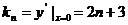 ,
,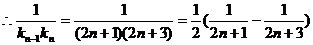
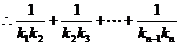
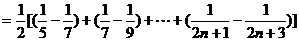
=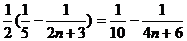
点评:本例为数列与解析几何的综合题,难度较大。(1)、(2)两问运用几何知识算出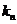 .
.
5.设 ,定义
,定义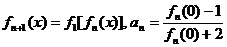 ,其中n∈N*.
,其中n∈N*.
(1)求数列{an}的通项公式;(2)若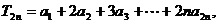 ,
,
解:(1) =2,
=2,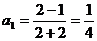 ,
,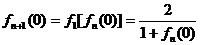 ,
,
∴
∴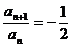 ,∴数列{an}上首项为
,∴数列{an}上首项为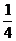 ,公比为
,公比为 的等比数列,
的等比数列,
(2)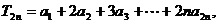
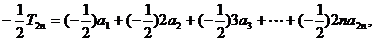
两式相减得: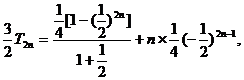
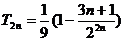
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com