
2.已知函数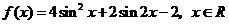 。
。
(1)求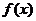 的最小正周期、
的最小正周期、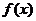 的最大值及此时x的集合;
的最大值及此时x的集合;
(2)证明:函数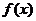 的图像关于直线
的图像关于直线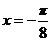 对称。
对称。
解: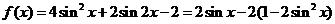
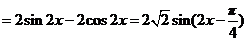
(1)所以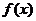 的最小正周期
的最小正周期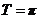 ,因为
,因为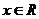 ,
,
所以,当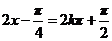 ,即
,即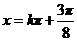 时,
时,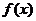 最大值为
最大值为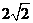 ;
;
(2)证明:欲证明函数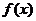 的图像关于直线
的图像关于直线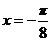 对称,只要证明对任意
对称,只要证明对任意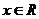 ,有
,有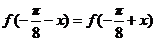 成立,
成立,
因为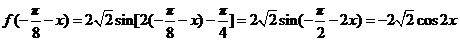 ,
,
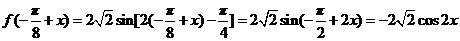 ,
,
所以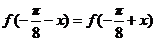 成立,从而函数
成立,从而函数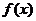 的图像关于直线
的图像关于直线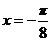 对称。
对称。
1.(广东卷)已知函数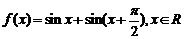 .(I)求
.(I)求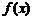 的最小正周期;
的最小正周期;
(II)求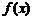 的的最大值和最小值;(III)若
的的最大值和最小值;(III)若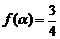 ,求
,求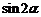 的值.
的值.
解: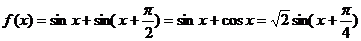
(Ⅰ)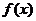 的最小正周期为
的最小正周期为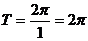 ; (Ⅱ)
; (Ⅱ)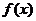 的最大值为
的最大值为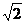 和最小值
和最小值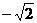 ;
;
(Ⅲ)因为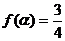 ,即
,即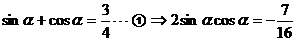 ,即
,即 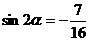
4.不等式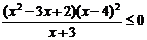 的解为
( D
)
的解为
( D
)
A.-1<x≤1或x≥2B.x<-3或1≤x≤2 C.x=4或-3<x≤1或x≥2D.x=4或x<-3或1≤x≤2
3.下列不等式中,解集为R的是 ( B )
A.|x-3|>x-3
B.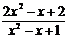 > 1 C.
> 1 C.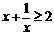 D.
D.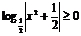
2.设a<0,则关于x的不等式42x2+ax-a2<0的解集为:( A )
(A)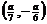 (B)
(B)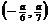 (C){0} (D) 无解
(C){0} (D) 无解
1. 已知R为全集,A={x|log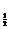 (3-x) ≥-2},B={x|
(3-x) ≥-2},B={x|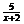 ≥1},
≥1},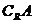 ∩B=( B
)
∩B=( B
)
(A)-2<x<-1 (B)–2<x<-1或x=3 (C)-2≤x<-1 (D)-2≤x≤1
3。大题形式多样与其他知识结合,不会出现单独的不等式题。
[问题1]不等式的解法
2.不等式组与线性规划。
18.(山东卷)已知数列{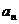 }中,
}中,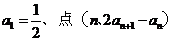 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令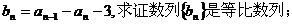 (Ⅱ)求数列
(Ⅱ)求数列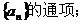
(Ⅲ)设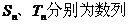
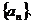
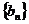 的前n项和,是否存在实数
的前n项和,是否存在实数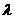 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出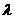 .若不存在,则说明理由。
.若不存在,则说明理由。
解:(I)由已知得 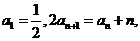
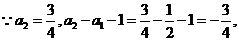
又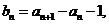
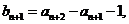
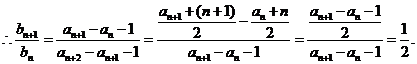
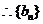 是以
是以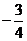 为首项,以
为首项,以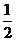 为公比的等比数列.
为公比的等比数列.
(II)由(I)知,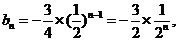
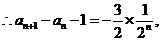
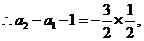
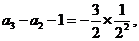
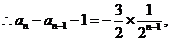
将以上各式相加得:
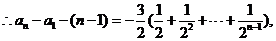
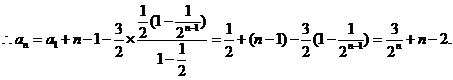
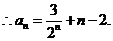
(III)解法一:
存在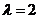 ,使数列
,使数列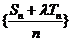 是等差数列.
是等差数列.
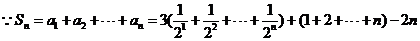
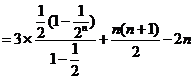
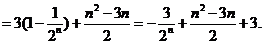
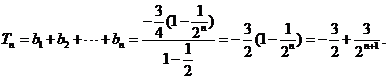
数列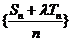 是等差数列的充要条件是
是等差数列的充要条件是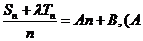 、
、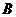 是常数
是常数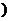
即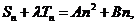
又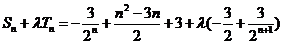

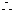 当且仅当
当且仅当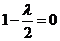 ,即
,即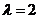 时,数列
时,数列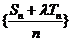 为等差数列.
为等差数列.
解法二:
存在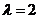 ,使数列
,使数列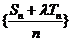 是等差数列.
是等差数列.
由(I)、(II)知,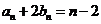
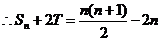
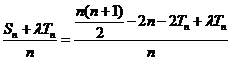
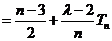
又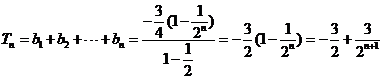
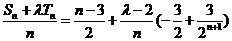
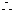 当且仅当
当且仅当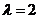 时,数列
时,数列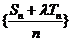 是等差数列.
是等差数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com