
6.函数y=cosx(sinx+cosx)的最小正周期为
A 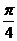 B
B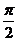 C
C 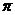 D
D 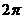
5.在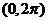 内,使
内,使 成立的
成立的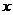 的取值范围是
的取值范围是
(A)(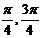 ) (B)(
) (B)( ) (C)(
) (C)(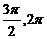 ) (D)(
) (D)(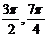 )
)
4.把函数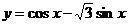 的图象沿向量
的图象沿向量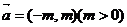 的方向平移后,所得的图象关于y轴对称,则m的最小值是
A.
的方向平移后,所得的图象关于y轴对称,则m的最小值是
A.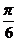 B.
B.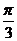 C.
C.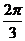 D.
D.
3.若函数f(x)同时具有以下两个性质:①f(x)是偶函数,②对任意实数x,都有f(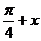 )= f(
)= f(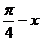 ),则f(x)的解析式可以是 A.f(x)=cosx B.f(x)=cos(2x
),则f(x)的解析式可以是 A.f(x)=cosx B.f(x)=cos(2x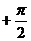 ) C.f(x)=sin(4x
) C.f(x)=sin(4x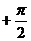 ) D.f(x) =cos6x
) D.f(x) =cos6x
2.已知 ,那么
,那么 A.
A.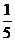 B.
B. 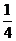 C.
C. 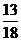 D.
D. 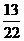
1.设函数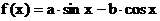 图象的一条对称轴方程为
图象的一条对称轴方程为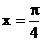 , 则直线
, 则直线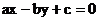 的倾斜角为
的倾斜角为
A.  B.
B. 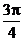 C.
C. 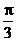 D.
D. 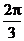
6. 已知函数y=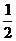 cos2x+
cos2x+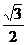 sinx·cosx+1 (x∈R),
sinx·cosx+1 (x∈R),
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图像可由y=sinx(x∈R)的图像经过怎样的平移和伸缩变换得到?
解:(1)y=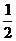 cos2x+
cos2x+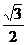 sinx·cosx+1=
sinx·cosx+1=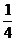 (2cos2x-1)+
(2cos2x-1)+ 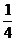 +
+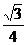 (2sinx·cosx)+1
(2sinx·cosx)+1
=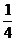 cos2x+
cos2x+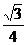 sin2x+
sin2x+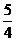 =
=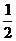 (cos2x·sin
(cos2x·sin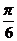 +sin2x·cos
+sin2x·cos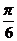 )+
)+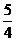
=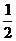 sin(2x+
sin(2x+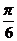 )+
)+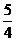
所以y取最大值时,只需2x+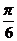 =
=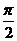 +2kπ,(k∈Z),即
x=
+2kπ,(k∈Z),即
x=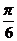 +kπ,(k∈Z)。
+kπ,(k∈Z)。
所以当函数y取最大值时,自变量x的集合为{x|x=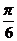 +kπ,k∈Z}
+kπ,k∈Z}
(2)将函数y=sinx依次进行如下变换:
(i)把函数y=sinx的图像向左平移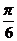 ,得到函数y=sin(x+
,得到函数y=sin(x+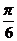 )的图像;
)的图像;
(ii)把得到的图像上各点横坐标缩短到原来的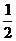 倍(纵坐标不变),得到函数y=sin(2x+
倍(纵坐标不变),得到函数y=sin(2x+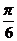 )的图像;
)的图像;
(iii)把得到的图像上各点纵坐标缩短到原来的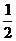 倍(横坐标不变),得到函数y=
倍(横坐标不变),得到函数y=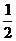 sin(2x+
sin(2x+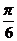 )的图像;
)的图像;
(iv)把得到的图像向上平移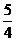 个单位长度,得到函数y=
个单位长度,得到函数y=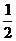 sin(2x+
sin(2x+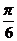 )+
)+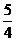 的图像。
的图像。
综上得到y=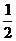 cos2x+
cos2x+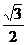 sinxcosx+1的图像。
sinxcosx+1的图像。
5.已知函数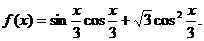
(Ⅰ)将f(x)写成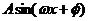 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
解: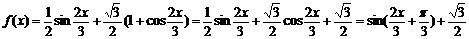
(Ⅰ)由 =0即
=0即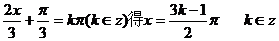
即对称中心的横坐标为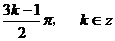
(Ⅱ)由已知b2=ac
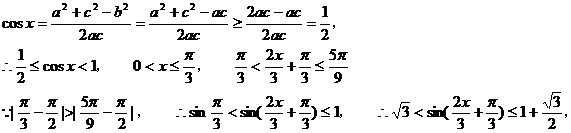 即
即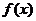 的值域为
的值域为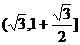 .
.
综上所述,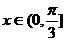 ,
,
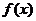 值域为
值域为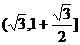 .
.
说明:本题综合运用了三角函数、余弦定理、基本不等式等知识,还需要利用数形结合的思想来解决函数值域的问题,有利于培养学生的运算能力,对知识进行整合的能力。
4.(重庆卷)设函数f(x)=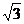 cos2ωx+sin
cos2ωx+sin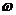 xcos
xcos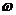 x+a(其中
x+a(其中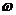 >0,a
>0,a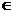 R),且f(x)的图象在y轴右侧的第一个高点的横坐标为
R),且f(x)的图象在y轴右侧的第一个高点的横坐标为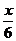 .(Ⅰ)求ω的值;(Ⅱ)如果f(x)在区间
.(Ⅰ)求ω的值;(Ⅱ)如果f(x)在区间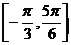 上的最小值为
上的最小值为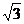 ,求a的值.
,求a的值.
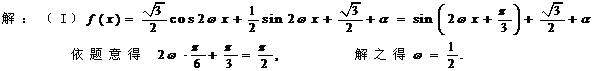
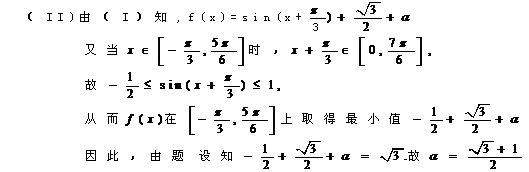
3.(上海春)已知函数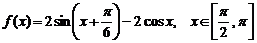 .
.
(1)若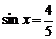 ,求函数
,求函数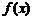 的值; (2)求函数
的值; (2)求函数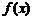 的值域.
的值域.
解:(1)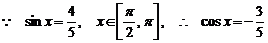 ,
,
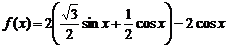
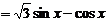
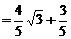 .
.
(2)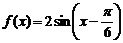
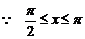
 ,
, 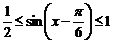 ,
,
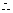 函数
函数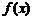 的值域为
的值域为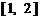 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com